题目内容
给出下列四个命题:
①若a<b,则a2<b2;
②若a≥b>-1,则
≥
;
③若正整数m和n满足m<n,则
≤
;
④若x>0,且x≠1,则lnx+
≥2.
其中所有真命题的序号是 .
①若a<b,则a2<b2;
②若a≥b>-1,则
| a |
| 1+a |
| b |
| 1+b |
③若正整数m和n满足m<n,则
| m(n-m) |
| n |
| 2 |
④若x>0,且x≠1,则lnx+
| 1 |
| lnx |
其中所有真命题的序号是
考点:命题的真假判断与应用
专题:计算题,简易逻辑
分析:①④列举反例,②③利用综合法证明即可.
解答:
解:①取a=-2,b=-1,则a2<b2不成立;
②若a≥b>-1,则1+a≥1+b>0,∵a+ab≥b+ab,∴
≥
,正确;
③若正整数m和n满足m<n,则
≤
=
,正确;
④若0<x<1,则lnx+
≤-2,故不正确.
故答案为:②③.
②若a≥b>-1,则1+a≥1+b>0,∵a+ab≥b+ab,∴
| a |
| 1+a |
| b |
| 1+b |
③若正整数m和n满足m<n,则
| m(n-m) |
| m+n-m |
| 2 |
| n |
| 2 |
④若0<x<1,则lnx+
| 1 |
| lnx |
故答案为:②③.
点评:正确的命题需要证明,不正确的命题列举反例即可.

练习册系列答案
相关题目
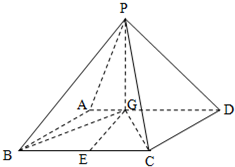 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=