题目内容
已知p：（x+2）（x-10）＞0，q：[x-（1-m）][x-（1+m）]≤0，（m＞0），若q是￢p的充分不必要条件，求实数m的取值范围．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：解不等式可得￢p：-2≤x≤10，q：1-m≤x≤1+m，由q是￢p的充分不必要条件可得m的不等式组，解不等式组可得．
解答：
解：∵p：（x+2）（x-10）＞0，
∴p：x＜-2或x＞10，
∴￢p：-2≤x≤10，
∵q：[x-（1-m）][x-（1+m）]≤0，（m＞0）
∴q：1-m≤x≤1+m，
∵q是￢p的充分不必要条件，
∴
，解得0＜m≤3，
∴实数m的取值范围为（0，3]
∴p：x＜-2或x＞10，
∴￢p：-2≤x≤10，
∵q：[x-（1-m）][x-（1+m）]≤0，（m＞0）
∴q：1-m≤x≤1+m，
∵q是￢p的充分不必要条件，
∴
|
∴实数m的取值范围为（0，3]
点评：本题考查充要条件，涉及不等式组的解集，属基础题．
练习册系列答案
相关题目
在两个袋内，分别装着写有0，1，2，3，4，5六个数字的6张卡片，今从每个袋中各任取一张卡片，则两数之和等于5的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
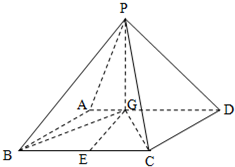如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上且AG=