题目内容
已知抛物线C:y2=2px(p>0)过点P(1,-2).
(Ⅰ)求抛物线C的方程,并求其准线方程;
(Ⅱ)过焦点F且斜率为2的直线l与抛物线交于A,B两点,求△OAB的面积.
(Ⅰ)求抛物线C的方程,并求其准线方程;
(Ⅱ)过焦点F且斜率为2的直线l与抛物线交于A,B两点,求△OAB的面积.
考点:直线与圆锥曲线的关系,抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)通过点的坐标适合方程求抛物线C的方程,并求其准线方程;
(Ⅱ)过焦点F且斜率为2的直线l,设出直线方程,利用过焦点F且斜率为2的直线l与抛物线交于A,B两点,联立方程组,利用韦达定理弦长公式以及点到直线的距离求出△OAB的面积.
(Ⅱ)过焦点F且斜率为2的直线l,设出直线方程,利用过焦点F且斜率为2的直线l与抛物线交于A,B两点,联立方程组,利用韦达定理弦长公式以及点到直线的距离求出△OAB的面积.
解答:
(本小题满分(13分),(Ⅰ)小问(5分),(Ⅱ)小问8分)
解:(Ⅰ)由题意:4=2p,解得:p=2,
从而抛物线的方程为y2=4x,准线方程为x=-1…(5分)
(Ⅱ)抛物线焦点坐标为F(1,0),依题意可设直线y=2x-2…(6分)
设点A(x1,y1),B(x2,y2)
联立
得:4x2-12x+4=0,即x2-3x+1=0…(8分)
设点A(x1,y1),B(x2,y2),则由韦达定理有:x1+x2=3,x1x2=1…(9分)
则弦长|AB|=
|x1-x2|=
•
=
•
=5…(11分)
而原点O(0,0)到直线l的距离d=
…(12分)
故S△FAB=
×|AB|×d=
…(13分)
解:(Ⅰ)由题意:4=2p,解得:p=2,
从而抛物线的方程为y2=4x,准线方程为x=-1…(5分)
(Ⅱ)抛物线焦点坐标为F(1,0),依题意可设直线y=2x-2…(6分)
设点A(x1,y1),B(x2,y2)
联立
|
设点A(x1,y1),B(x2,y2),则由韦达定理有:x1+x2=3,x1x2=1…(9分)
则弦长|AB|=
| 5 |
| 5 |
| (x1+x2)2-4x1x2 |
| 5 |
| 9-4 |
而原点O(0,0)到直线l的距离d=
| 2 |
| 5 |
| 5 |
故S△FAB=
| 1 |
| 2 |
| 5 |
点评:本题考查直线与抛物线的位置关系的应用,抛物线的方程的求法以及性质的应用,考查计算能力.

练习册系列答案
相关题目
曲线f(x)=x2+x+1在点(0,1)处的切线方程为( )
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |
在两个袋内,分别装着写有0,1,2,3,4,5六个数字的6张卡片,今从每个袋中各任取一张卡片,则两数之和等于5的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
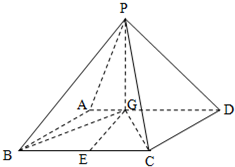 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=