题目内容
在区间（0，+∞）上递增的函数是（ ）
A、y=(
| ||
| B、y=log2x | ||
C、y=log
| ||
| D、y=x-1． |
考点：函数单调性的性质
专题：函数的性质及应用
分析：对不同的基本初等函数判断在同一区间上的单调性的问题，结合选项逐一进行排查，考虑所给函数的特性，验证它们的单调性即可．
解答：
解：在A中，y=(
)x，是底数小于1的指数函数，在区间（0，+∞）上是减函数；
在B中，y=log2x定义域是（0，+∞），底数大于1的对数函数，在区间（0，+∞）上是增函数；
在C中，y=log
x定义域是（0，+∞），底数小于1的对数函数，在区间（0，+∞）上是减函数；
在D中，y=x-1，是反比例，图象是双曲线，在区间（0，+∞）上是减函数；
故选：B．
| 1 |
| 2 |
在B中，y=log2x定义域是（0，+∞），底数大于1的对数函数，在区间（0，+∞）上是增函数；
在C中，y=log
| 1 |
| 2 |
在D中，y=x-1，是反比例，图象是双曲线，在区间（0，+∞）上是减函数；
故选：B．
点评：本题考查了对不同的基本初等函数判断在同一区间上的单调性的问题，在解答时，结合选项逐一进行排查，是基础题．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
定义a?b=
，则函数f（x）=x?（2-x）的值域是（ ）
|
| A、（-∞，1） | B、（-∞，1] |
| C、R | D、（1，+∞） |
函数f（x）=2x+x的零点所在的区间为（ ）
| A、（-2，-1） |
| B、（-1，0） |
| C、（0，1） |
| D、（1，2） |
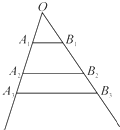如图，互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上，所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．设OAn=an，若a1=1，a2=2，则a9=（ ）A、
| ||
B、
| ||
| C、5 | ||
D、2
|
已知|
|=1，|
|=2，
与
的夹角为120°，则
+
在
方向上的投影为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、0 | B、1 | C、-1 | D、2 |
给定下列两个命题：
①“p∨q”为真是“?p”为假的必要不充分条件；
②“?x∈R，使sinx＞0”的否定是“?x∈R，使sinx≤0”．
其中说法正确的是（ ）
①“p∨q”为真是“?p”为假的必要不充分条件；
②“?x∈R，使sinx＞0”的否定是“?x∈R，使sinx≤0”．
其中说法正确的是（ ）
| A、①真②假 |
| B、①假②真 |
| C、①和②都为假 |
| D、①和②都为真 |
函数y=
与y=tanx的图象交点的个数为（ ）
| π2-x2 |
| A、1 | B、2 | C、3 | D、4 |
在△ABC中，A=60°，AB=1，AC=2，则S△ABC的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
中山路上有A，B，C三处设有交通灯，这三盏灯在一分钟内开放绿灯的时间分别为25秒，35秒，45秒，某辆车在中山路上行驶，则在三处都不停车的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|