题目内容
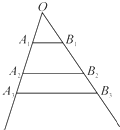 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=( )
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=( )A、
| ||
B、
| ||
| C、5 | ||
D、2
|
考点:平行线分线段成比例定理
专题:立体几何
分析:本题可以根据所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.然后利用所有的三角形都相似,面积比等于相似比的平方,得出一系列的等式,然后利用累乘法求得通项,进一步求得结果.
解答:
解:依题意:互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上.
则令s△OA1B1=m(m>0)
∵所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.
∴利用所有的三角形都相似,面积比等于相似比的平方
若a1=1,a2=2,则令s△OA1B1=m(m>0)
∴s梯形A1B1A2B2=3m
∴当n≥2时
=
=
=
故
=
=
…
=
以上各式累乘可得:
=(3n-2
由于a1=1
∴an=
∴a9=5
故选:C
则令s△OA1B1=m(m>0)
∵所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.
∴利用所有的三角形都相似,面积比等于相似比的平方
若a1=1,a2=2,则令s△OA1B1=m(m>0)
∴s梯形A1B1A2B2=3m
∴当n≥2时
| an |
| an-1 |
| OAn |
| OAn-1 |
|
|
故
| a | 2 n |
| 2 n-1 |
| a | 2 n-1 |
| 3n-5 |
| 3n-8 |
| a | 2 n-2 |
…
| a | 2 2 |
| 2 1 |
以上各式累乘可得:
| a | 2 n |
| )a | 2 1 |
∴an=
| 3n-2 |
∴a9=5
故选:C
点评:本题应用知识较多:平行线分线段成比例定理,相似三角形面积比等于相似比的平方,数列通项中的累乘法,

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
定义区间(m,n),[m,n],[m,n),(m,n]的长度均为n-m,其中n>m,已知关于实数x的不等式组
的解集构成的各区间长度之和为4,则实数t的取值范围是( )
|
A、(0,
| ||
B、(0,
| ||
C、(0,
| ||
D、(0,
|
函数f(x)=lg(3-2x-x2)的定义域为P,值域为Q,则P∩Q=( )
| A、(-∞,lg4] |
| B、(-3,1) |
| C、(-3,lg4] |
| D、(-1,lg4) |
已知甲:x≥0,乙:|x-1|<1.则甲是乙的( )
| A、必要非充分条件 |
| B、充分非必要条件 |
| C、即不必要也不充分条件 |
| D、充要分条件 |
若a,b是任意实数,且a>b,则下列不等式正确的是( )
| A、a2>b2 | ||
B、
| ||
| C、lg(a-b)>0 | ||
| D、b<a |
在区间(0,+∞)上递增的函数是( )
A、y=(
| ||
| B、y=log2x | ||
C、y=log
| ||
| D、y=x-1. |
函数y=
在(0,+∞)上( )
| 1 |
| x |
| A、既无最大值又无最小值 |
| B、仅有最小值 |
| C、既有最大值又有最小值 |
| D、仅有最大值 |
设函数f(x)=ln(1+x)-x,记a=f(1),b=f(
),c=f(
),则( )
| 3 |
| 7 |
| A、b<a<c |
| B、c<b<a |
| C、a<b<c |
| D、a<c<b |