题目内容
14.在△ABC中,角A,B,C所对的边分别是a,b,c且a=3,b=$\sqrt{3}$,面积为$\frac{3\sqrt{3}}{4}$,则边c的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{21}$ | C. | $\sqrt{3}$或$\sqrt{21}$ | D. | $\sqrt{6}$ |
分析 根据题目的已知条件,利用三角形的面积公式,求出sinC,可得cosC,利用余弦定理,即可得出结论.
解答 解:∵△ABC中,角A,B,C所对的边分别是a,b,c且a=3,b=$\sqrt{3}$,面积为$\frac{3\sqrt{3}}{4}$,
∴$\frac{1}{2}×3×\sqrt{3}×sinC$=$\frac{3\sqrt{3}}{4}$,
∴sinC=$\frac{1}{2}$,
∴cosC=±$\frac{\sqrt{3}}{2}$,
∴c=$\sqrt{9+3-2×3×\sqrt{3}×(±\frac{\sqrt{3}}{2})}$=$\sqrt{3}$或$\sqrt{21}$.
故选:C.
点评 本题是基础题,考查三角形的边角关系,三角形的求解方法,三角形的面积公式的应用,考查计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
4.程序框图如图所示,则该程序运行后输出的值是( )
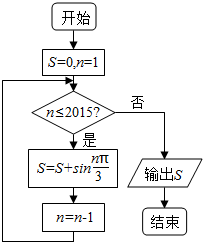

| A. | 0 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
6.若i是虚数单位,a,b∈R,且i•[a+(b-2)i]=1+i,则a+b的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
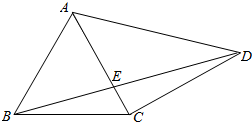 如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$
如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$