题目内容
19.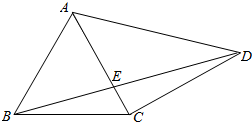 如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$
如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$(Ⅰ)求∠BEA的度数;
(Ⅱ)求BD及AE的长.
分析 (1)∠BCD=90°+60°=150°,△BCD是等腰三角形,得出∠DBC=15°,根据三角形外角的性质得出∠BEA=75°;
(2)在△BCD中,利用余弦定理解出BD,在△ABE中利用正弦定理解出AE.
解答 解:(Ⅰ)因为△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°
∴∠BCD=90°+60°=150°,
∵CB=AC=CD,∴∠CBD=15°.
所以∠BEA=∠CBE+∠BCE=15°+60°=75°.
(Ⅱ)在△BCD中,由余弦定理得:BD2=CB2+CD2-2CB•CD•cos∠BCD=$2+2-2\sqrt{2}•\sqrt{2}•(-\frac{{\sqrt{3}}}{2})$=$4+2\sqrt{3}$=${(\sqrt{3}+1)^2}$
∴$BD=\sqrt{3}+1$.
在△ABE中,由正弦定理得:$\frac{AE}{sin∠ABE}=\frac{AB}{sin∠AEB}$
即$\frac{AE}{{sin({{60}°}-{{15}°})}}=\frac{{\sqrt{2}}}{{sin{{75}°}}}$.
故$AE=\frac{{\sqrt{2}sin{{45}°}}}{{sin{{75}°}}}$=$\frac{{\sqrt{2}×\frac{{\sqrt{2}}}{2}}}{{\frac{{\sqrt{6}+\sqrt{2}}}{4}}}$=$\sqrt{6}-\sqrt{2}$.
点评 本题考查了利用正余弦定理解三角形,寻找合适的三角形是解题关键.

练习册系列答案
相关题目
10.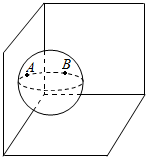 一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )
一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )
 一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )
一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )| A. | 20cm | B. | 40cm | C. | 28.3cm | D. | 34.6cm |
14.在△ABC中,角A,B,C所对的边分别是a,b,c且a=3,b=$\sqrt{3}$,面积为$\frac{3\sqrt{3}}{4}$,则边c的长为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{21}$ | C. | $\sqrt{3}$或$\sqrt{21}$ | D. | $\sqrt{6}$ |
11.在等差数列{an}中,若a2=4,a5=1,则a9=( )
| A. | 4 | B. | -3 | C. | -2 | D. | -1 |
8.设实数a=log32,b=log0.84,c=20.3,则( )
| A. | a>c>b | B. | b>c>a | C. | c>b>a | D. | c>a>b |