题目内容
在△ABC中,A,B,C的对边分别为a,b,c,且a,b,c依次成等差数列.
(Ⅰ)若向量
=(3,sinB)与
=(2,sinC)共线,求cosA的值;
(Ⅱ)若ac=8,求△ABC的面积S的最大值.
(Ⅰ)若向量
| m |
| n |
(Ⅱ)若ac=8,求△ABC的面积S的最大值.
考点:等差数列的性质,平面向量数量积的运算,正弦定理,余弦定理
专题:综合题,解三角形,平面向量及应用
分析:(Ⅰ)利用a,b,c依次成等差数列,可得2b=a+c,由向量
=(3,sinB)与
=(2,sinC)共线,可得2sinB=3sinC,由正弦定理可得2b=3c,所以a=2c,b=
c,利用余弦定理可求cosA的值;
(Ⅱ)先确定0<sinB≤
,再求△ABC的面积S的最大值.
| m |
| n |
| 3 |
| 2 |
(Ⅱ)先确定0<sinB≤
| ||
| 2 |
解答:
解:(Ⅰ)∵a,b,c依次成等差数列,∴2b=a+c.
∵向量
=(3,sinB)与
=(2,sinC)共线,
∴2sinB=3sinC,
∴由正弦定理可得2b=3c,∴a=2c,b=
c,
∴cosA=
=-
;
(Ⅱ)∵2b=a+c,
∴cosB=
=
≥
=
,
∵B∈[0,π],
∴0<sinB≤
,
∴S=
acsinB≤
×8×
=2
,
∴△ABC的面积S的最大值为2
.
∵向量
| m |
| n |
∴2sinB=3sinC,
∴由正弦定理可得2b=3c,∴a=2c,b=
| 3 |
| 2 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 4 |
(Ⅱ)∵2b=a+c,
∴cosB=
| a2+c2-b2 |
| 2ac |
| 3a2+3c2-2ac |
| 8ac |
| 4ac |
| 8ac |
| 1 |
| 2 |
∵B∈[0,π],
∴0<sinB≤
| ||
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴△ABC的面积S的最大值为2
| 3 |
点评:本题考查等差数列的性质,考查向量知识的运用,考查正弦定理、余弦定理,考查基本不等式的运用,综合性强.

练习册系列答案
相关题目
已知三点A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2,且0≤
•
≤2,则点P到点C的距离大于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
已知集合A={x|x2-x<0},集合B={x|2x<4},则“x∈A”是“x∈B”的( )
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
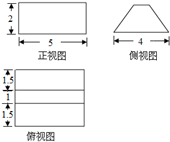

A、
| ||
| B、50cm3 | ||
C、
| ||
| D、25cm3 |
执行如图所示的程序框图,若输入n的值为4,则输出s的值是( )


| A、2 | B、6 | C、24 | D、120 |