题目内容
函数f（x）=a（x+1）+2（a＞0且a≠1），必经过定点 ．
考点：指数函数的单调性与特殊点
专题：函数的性质及应用
分析：令x+1=0，由函数的解析式求得x和y的值，可得函数f（x）=a（x+1）+2的图象恒过的定点的坐标．
解答：
解：令x+1=0，由函数的解析式求得x=-1且y=3，
故函数f（x）=a（x+1）+2的图象恒过定点（-1，3），
故答案为：（-1，3）
故函数f（x）=a（x+1）+2的图象恒过定点（-1，3），
故答案为：（-1，3）
点评：本题主要考查指数函数的单调性和特殊点，属于基础题．
练习册系列答案
优加精卷系列答案
相关题目
一次数学测验后某班成绩均在（20，100]区间内，统计后画出的频率分布直方图如图，如分数在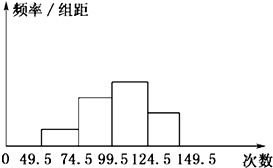
为了了解小学生的体能情况，抽取了某校一个年级的部分学生进行一分钟跳绳次数测试，将取得的数据整理后，画出频率分布直方图（如图）．已知图中从左到右前三个小组的频率分别为0.1，0.3，0.4，且第一小组的频数为5．执行如图所示的程序框图，如果输出的结果为
，则判断框内可填入的条件是（ ）
| 31 |
| 16 |
| A、k＜4 | B、k＞4 |
| C、k＜5 | D、k＞5 |