题目内容
设U=R,A={x|mx2+8mx+21>0},∁UA=∅,则m的取值范围是( )
A、0≤m<
| ||
B、m>
| ||
| C、m≤0 | ||
D、m≤0或m>
|
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由题意和补集的运算求出集合A,由A中元素的性质得mx2+8mx+21>0恒成立,对m进行分类讨论,利用二次函数的性质求出m的范围,最后并在一起.
解答:
解:由∁UA=∅得A=R,即mx2+8mx+21>0恒成立,
当m=0时,不等式恒成立;
当m≠0时,则
,解得0<m<
,
所以m的取值范围为[0,
).
故选:A.
当m=0时,不等式恒成立;
当m≠0时,则
|
| 21 |
| 16 |
所以m的取值范围为[0,
| 21 |
| 16 |
故选:A.
点评:本题考查补集及其运算,利用二次函数的性质解决不等式的恒成立问题,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
执行如图所示的程序框图,如果输出的结果为
,则判断框内可填入的条件是( )

| 31 |
| 16 |

| A、k<4 | B、k>4 |
| C、k<5 | D、k>5 |
下列运算正确的是( )
| A、a3•a2=a6 |
| B、a8÷a2=a4 |
| C、(ab3)3=ab9 |
| D、(a3)2=a6 |
命题“若x>2,则x>1”的逆命题是( )
| A、若x>1,则x>2 |
| B、若x≤2,则x≤1 |
| C、若x≤1,则x≤2 |
| D、若x<2,则x<1 |
已知集合A={x|x>0},则命题“任意x∈A,x2-|x|>0”的否定是( )
| A、任意x∈A,x2-|x|≤0 |
| B、任意x∉A,x2-|x|≤0 |
| C、存在x∉A,x2-|x|>0 |
| D、存在x∈A,x2-|x|≤0 |
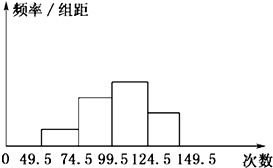 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.