题目内容
如图,给出奇函数f(x)的局部图象,则使f(x)<0的x的集合是 .


考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:由题意,x>0时f(x)<0可得0<x<2;再由奇函数知x<0时,f(x)<0可得x<-2;从而得不等式的解集.
解答:
解:由题意可得,x>0时f(x)<0可得0<x<2;
再由奇函数知x<0时,f(x)<0可得x<-2;
故使f(x)<0的x的集合是(-∞,-2)∪(0,2);
故答案为:(-∞,-2)∪(0,2).
再由奇函数知x<0时,f(x)<0可得x<-2;
故使f(x)<0的x的集合是(-∞,-2)∪(0,2);
故答案为:(-∞,-2)∪(0,2).
点评:本题考查了函数的图象与函数的奇偶性的应用,属于基础题.

练习册系列答案
相关题目
抛物线y=4ax2(a≠0)的焦点坐标是( )
| A、(0,a) | ||
| B、(a,0) | ||
C、(0,
| ||
D、(
|
方程
=|x-y+3|表示的曲线是( )
| 2(x+3)2+2(y-1)2 |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
若loga
<1,则a的取值范围是( )
| 2 |
| 3 |
A、0<a<
| ||
B、a>
| ||
C、
| ||
D、0<a<
|
下列运算正确的是( )
| A、a3•a2=a6 |
| B、a8÷a2=a4 |
| C、(ab3)3=ab9 |
| D、(a3)2=a6 |
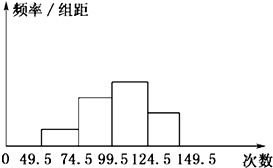 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.