题目内容

已知曲线y=
1
6
x2-1与y=1+x3在x=x0处的切线互相垂直，则x0的值为
 
．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出两个函数的导数，通过求出在x=x0处的切线的斜率的乘积为-1，求出x0的值．
解答： 解：对于y=
1
6
x2-1，有y′=
1
3
x，k1=y′|x=x0=
1
3
x0；
对于y=1+x3，有y′=3x2，k2=y′|x=x0=3x02．
又k1k2=-1，则x03=-1，x0=-1．
故答案为：-1．
点评：本题考查函数的导数的应用，切线的斜率的求法，考查计算能力．
练习册系列答案
相关题目
已知函数f（x）的定义域为D，若存在闭区间[a，b]⊆D，使得函数f（x）满足：①f（x）在[a，b]内是单调函数；②f（x）在[a，b]上的值域为[2a，2b]，则称区间[a，b]为y=f（x）的“倍值区间”，下列函数中存在“倍值区间”的有
 
．
①f（x）=2x（x∈R）
②f（x）=x2（x≥0）
③f（x）=ex（x∈R）
④f（x）=lnx（x＞0）
一次数学测验后某班成绩均在（20，100]区间内，统计后画出的频率分布直方图如图，如分数在
（60，70]分数段内有9人．则此班级的总人数为
 
．
下列说法正确的个数为（　　）
①彩票的中奖率为千分之一，那么买一千张彩票就肯定能中奖；
②概率为零的事件一定不会发生；
③抛掷一枚均匀的硬币，如前两次都是反面，那么第三次出现正面的可能性就比反面大；
④在袋子中放有2白2黑大小相同的四个小球，甲乙玩游戏的规则是从中不放回的依次随机摸出两个小球，如两球同色则甲获胜，否则乙获胜，那么这种游戏是公平的．
A、1B、2C、3D、0
方程
2(x+3)2+2(y-1)2
=|x-y+3|表示的曲线是（　　）
A、圆B、椭圆C、双曲线D、抛物线
双曲线
y2
16
-
x2
4
=1上一点P到它的一个焦点的距离等于1，那么点P到另一个焦点的距离为（　　）
A、5B、7C、9D、17
已知等比数列{an}的公比q=-
1
2
，a3=
1
4
．
（1）求数列{an}的通项公式；
（2）求数列{an}的前n项和．
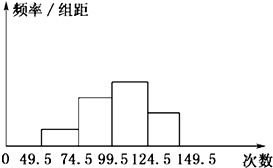为了了解小学生的体能情况，抽取了某校一个年级的部分学生进行一分钟跳绳次数测试，将取得的数据整理后，画出频率分布直方图（如图）．已知图中从左到右前三个小组的频率分别为0.1，0.3，0.4，且第一小组的频数为5．
（1）求第四小组的频率；
（2）参加这次测试的学生一共有多少人？
（3）若次数在75次以上（含75次）为达标，试估计该年级学生在跳绳测试中的达标率是多少？
执行如图所示的程序框图，如果输出的结果为
31
16
，则判断框内可填入的条件是（　　）
A、k＜4B、k＞4
C、k＜5D、k＞5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网