题目内容
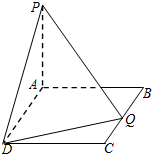 如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t
如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t(1)若在边BC上存在一点Q,使PQ⊥QD,求a与t关系;
(2)在(1)的条件下求a的取值范围;
(3)(理科做,文科不做)当边BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值.
考点:二面角的平面角及求法
专题:空间角
分析:(1)利用直角三角形的勾股定理得到a,t的关系;
(2)利用(1)的结论结合基本不等式求a的范围;
(3)由(Ⅰ)知,当t=2,a=4时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
过Q作QM∥CD交AD于M,则QM⊥AD.得到平面角∠MNQ是二面角A-PD-Q的平面角,结合直角三角形的余弦求之.
(2)利用(1)的结论结合基本不等式求a的范围;
(3)由(Ⅰ)知,当t=2,a=4时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
过Q作QM∥CD交AD于M,则QM⊥AD.得到平面角∠MNQ是二面角A-PD-Q的平面角,结合直角三角形的余弦求之.
解答:
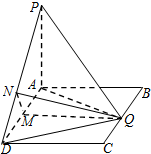 解:(1)如图,连接AQ,由于PA⊥平面ABCD,则由PQ⊥QD,必有AQ⊥DQ.
解:(1)如图,连接AQ,由于PA⊥平面ABCD,则由PQ⊥QD,必有AQ⊥DQ.
设,则CQ=a-t,
在直角三角形MBQ中中,有AQ=
.
在Rt△CDQ中,有DQ=
. …(4分)
在Rt△ADQ中,有AQ2+DQ2=AD2.
即t2+4+(a-t)2+4=a2,
即t2-at+4=0.
(2)由(1)得a=t+
≥4.
故a的取值范围为[4,+∞).
(3)由(Ⅰ)知,当t=2,a=4时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
过Q作QM∥CD交AD于M,则QM⊥AD.
∵PA⊥平面ABCD,∴PA⊥QM.∴QM⊥平面PAD.
过M作MN⊥PD于N,连结NQ,则QN⊥PD.
∴∠MNQ是二面角A-PD-Q的平面角.
在等腰直角三角形PAD中,可求得MN=
,又MQ=2,进而NQ=
.
∴cos∠MNQ=
=
=
.
故二面角A-PD-Q的余弦值为
.
 解:(1)如图,连接AQ,由于PA⊥平面ABCD,则由PQ⊥QD,必有AQ⊥DQ.
解:(1)如图,连接AQ,由于PA⊥平面ABCD,则由PQ⊥QD,必有AQ⊥DQ.设,则CQ=a-t,
在直角三角形MBQ中中,有AQ=
| t2+4 |
在Rt△CDQ中,有DQ=
| (a-t)2+4 |
在Rt△ADQ中,有AQ2+DQ2=AD2.
即t2+4+(a-t)2+4=a2,
即t2-at+4=0.
(2)由(1)得a=t+
| 4 |
| t |
故a的取值范围为[4,+∞).
(3)由(Ⅰ)知,当t=2,a=4时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
过Q作QM∥CD交AD于M,则QM⊥AD.
∵PA⊥平面ABCD,∴PA⊥QM.∴QM⊥平面PAD.
过M作MN⊥PD于N,连结NQ,则QN⊥PD.
∴∠MNQ是二面角A-PD-Q的平面角.
在等腰直角三角形PAD中,可求得MN=
| 2 |
| 6 |
∴cos∠MNQ=
| MN |
| NQ |
| ||
|
| ||
| 3 |
故二面角A-PD-Q的余弦值为
| ||
| 3 |
点评:本题考查了直角三角形的勾股定理以及二面角的平面角求法,关键在正确找出平面角,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
下列命题中正确的是( )
| A、一直线与一平面平行,这个平面内有无数条直线与它平行 |
| B、平行于同一直线的两个平面平行 |
| C、与两相交平面的交线平行的直线必平行于这两个相交平面 |
| D、两条平行直线中的一条与一个平面平行,则另一条也与该平面平行 |
正方体的外接球与其内切球的体积之比为 ( )
A、
| ||
| B、3:1 | ||
C、3
| ||
| D、9:1 |
已知椭圆
+
=1上一点A(2,1)和该椭圆上两动点B、C,直线AB、AC的斜率分别为k1、k2,且k1+k2=0,则直线BC的斜率k( )
| x2 |
| 8 |
| y2 |
| 2 |
A、k>
| ||||
B、k=-
| ||||
C、k=
| ||||
| D、k的值不确定 |
锐角△ABC中,角A,B,C所对的边分别为a,b,c,若C=2A,则
的取值范围是( )
| c |
| a |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
| D、(1,2) |
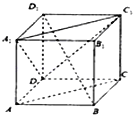 如图正方体ABCD-A1B1C1D1,下面结论正确的是
如图正方体ABCD-A1B1C1D1,下面结论正确的是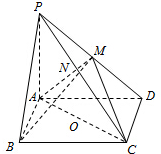 在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.