题目内容
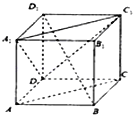 如图正方体ABCD-A1B1C1D1,下面结论正确的是
如图正方体ABCD-A1B1C1D1,下面结论正确的是①BD1⊥平面DA1C1
②过点B与异面直线AC和A1D所成角均为60°的有3条直线;
③四面体DA1D1C1与正方体ABCD-A1B1C1D1的内切球半径之比为
| ||
| 3 |
④与平面DA1C1平行的平面与正方体的各个面都有交点,则这个截面的周长为定值.
考点:命题的真假判断与应用
专题:空间位置关系与距离,空间角,简易逻辑
分析:①由于BD1⊥A1D,BD1⊥C1D,利用线面垂直的判定定理可得BD1⊥平面DA1C1;
②由于异面直线AC和A1D所成的角为60°,可得过点B与异面直线AC和A1D所成的角均为60°的直线有且只有2条.
③设AA1=a,可求得四面体DA1D1C1内切球半径为
a,而正方体ABCD-A1B1C1D1的内切球半径为
a,即可得出所求的比.
④将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,等于3
a(a为正方体的棱长).
②由于异面直线AC和A1D所成的角为60°,可得过点B与异面直线AC和A1D所成的角均为60°的直线有且只有2条.
③设AA1=a,可求得四面体DA1D1C1内切球半径为
| 1 | ||
3+
|
| 1 |
| 2 |
④将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,等于3
| 2 |
解答:
解:在正方体ABCD-A1B1C1D1 中,
①由正方体的性质可得BD1⊥A1C1,DC1⊥BD1,再根据直线和平面垂直的判定定理可得BD1⊥平面DA1C1,故①正确;
∵AC和A1D所成角均为60°,将A与A1D移至B点,可知过点B与异面直线AC和A1D所成角均为60°的有2条直线,故②错误;
 ③设AA1=a,可求得四面体DA1D1C1内切球半径为
③设AA1=a,可求得四面体DA1D1C1内切球半径为
a,而正方体ABCD-A1B1C1D1的内切球半径为
a,
故所求的比应为1-
.故③错误;
④将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,
等于3
a(a为正方体的棱长),故④正确.
综上可知:正确的有①、④.
故答案为:①④.
①由正方体的性质可得BD1⊥A1C1,DC1⊥BD1,再根据直线和平面垂直的判定定理可得BD1⊥平面DA1C1,故①正确;
∵AC和A1D所成角均为60°,将A与A1D移至B点,可知过点B与异面直线AC和A1D所成角均为60°的有2条直线,故②错误;
 ③设AA1=a,可求得四面体DA1D1C1内切球半径为
③设AA1=a,可求得四面体DA1D1C1内切球半径为| 1 | ||
3+
|
| 1 |
| 2 |
故所求的比应为1-
| ||
| 3 |
④将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,
等于3
| 2 |
综上可知:正确的有①、④.
故答案为:①④.
点评:本题综合考查了线面平行于垂直的判定定理和性质定理、异面直线所成的角、内切球的性质、展开图等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
若曲线y=
与直线y=kx+1有两个不同的交点,则实数k的取值范围是( )
|
A、(-3-2
| ||||
B、(-3+2
| ||||
C、(-∞,-3-2
| ||||
D、(-3-2
|
已知点P(8,8)在抛物线C:y2=2px(p>0)上,直线l与抛物线C相切于点P,则直线l的斜率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB和坡角α(长度精确到0.1m,角度精确到1°).
如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB和坡角α(长度精确到0.1m,角度精确到1°). 已知点
已知点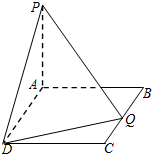 如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t
如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t