题目内容
锐角△ABC中,角A,B,C所对的边分别为a,b,c,若C=2A,则
的取值范围是( )
| c |
| a |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
| D、(1,2) |
考点:正弦定理的应用
专题:计算题,三角函数的求值,解三角形
分析:根据正弦定理可得到
=
,结合∠C=2∠A根据二倍角公式可得,
=
=
,整理得到
=2cosA,再求得A的范围即可得到取值范围.
| a |
| sinA |
| c |
| sinC |
| c |
| sin2A |
| a |
| sinA |
| c |
| 2sinAcosA |
| c |
| a |
解答:
解:由正弦定理
=
,
∵C=2A∴
=
=
,
∴
=2cosA,
当C为最大角时C<90°∴A<45°
当B为最大角时B<90°∴A>30°
∴30°<A<45°,
2cos45°<2cosA<2cos30°,
∴
∈(
,
)
故选A.
| a |
| sinA |
| c |
| sinC |
∵C=2A∴
| c |
| sin2A |
| a |
| sinA |
| c |
| 2sinAcosA |
∴
| c |
| a |
当C为最大角时C<90°∴A<45°
当B为最大角时B<90°∴A>30°
∴30°<A<45°,
2cos45°<2cosA<2cos30°,
∴
| c |
| a |
| 2 |
| 3 |
故选A.
点评:本题主要考查正弦定理和二倍角公式的应用.正弦定理和余弦定理在解三角形中应用比较多,这两个定理和其推论一定要熟练掌握并能够灵活运用.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
已知函数f(x)=
是R上的增函数,那么实数a的取值范围为( )
|
A、(
| ||
| B、(1,+∞) | ||
| C、[2,+∞) | ||
| D、(1,2) |
已知k∈[-2,1],则k的值使得过A(1,1)可以作两条直线与圆 x2+y2+kx-2y-
k=0相切的概率等于( )
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
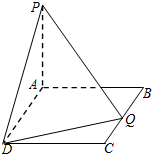 如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t
如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t