题目内容
曲线f(x)=cosx(x>0)上所有最值点按横坐标由小到大的顺序排成点列(an,f(an))(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=3nan,数列{bn}的前n项和为Tn,求sinT7的值.
(1)求数列{an}的通项公式;
(2)设bn=3nan,数列{bn}的前n项和为Tn,求sinT7的值.
考点:数列的求和,余弦函数的图象
专题:等差数列与等比数列,三角函数的求值
分析:(1)首先根据最值直接确定解析式,即通项公式.
(2)由(1)的结论利用乘公比错位相减法在数列求出前n项和,进一步求出三角函数值.
(2)由(1)的结论利用乘公比错位相减法在数列求出前n项和,进一步求出三角函数值.
解答:
解:(1)曲线f(x)=cosx(x>0)上所有最值点按横坐标由小到大的顺序排成点列(an,f(an))(n∈N*).
即令f(an)=±1
解得:an=nπ
(2)设bn=3nan
则:bn=n3nπ
Tn=b1+b2+…+bn-1+bn=(1•31+2•32+…+(n-1)•3n-1+n•3n)π①
3Tn=(1•32+2•33+…+(n-1)•3n+n•3n+1)π②
①-②得:
-2Tn=((31+32+33+…+3n)-n•3n+1)π
解得:
Tn=
+
sinT7=sin21324π=0
即令f(an)=±1
解得:an=nπ
(2)设bn=3nan
则:bn=n3nπ
Tn=b1+b2+…+bn-1+bn=(1•31+2•32+…+(n-1)•3n-1+n•3n)π①
3Tn=(1•32+2•33+…+(n-1)•3n+n•3n+1)π②
①-②得:
-2Tn=((31+32+33+…+3n)-n•3n+1)π
解得:
Tn=
| 3(1-3n)π |
| 4 |
| n3n+1π |
| 2 |
sinT7=sin21324π=0
点评:本题考查的知识要点:根据函数的最值确定通项公式,利用乘公比错位相减法在数列求和中的应用,三角函数值的求法.

练习册系列答案
相关题目
 如图,某几何体中,正三棱柱ABC-A′B′C′的所有棱长都为2,四边形ABCD是菱形,其中P为AC的中点.
如图,某几何体中,正三棱柱ABC-A′B′C′的所有棱长都为2,四边形ABCD是菱形,其中P为AC的中点. 如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB和坡角α(长度精确到0.1m,角度精确到1°).
如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB和坡角α(长度精确到0.1m,角度精确到1°).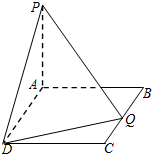 如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t
如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.BQ=t