题目内容
化简:
sin(
-α)-cos(
-α)= .
| 3 |
| π |
| 6 |
| π |
| 6 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:根据辅助角公式以及两角和差的正弦公式进行化简,即可得到结论.
解答:
解:
sin(
-α)-cos(
-α)=2[
sin(
-α)-
cos(
-α)]
=2[sin(
-α)cos
-sin
cos(
-α)]=2sin(
-α-
)=2sin(-α)=-2sinα,
故答案为:-2sinα
| 3 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
=2[sin(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
故答案为:-2sinα
点评:本题主要考查三角函数式的化简,利用辅助角公式以及两角和差的正弦公式是解决本题的关键,考查学生的运算能力.

练习册系列答案
相关题目
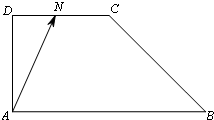 如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=
如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=