题目内容
设A∪B∪C={1,2,3,4,5,6},且A∩B={1,2},{1,2,3,4}⊆B∪C,则符合条件的(A,B,C)共有 组.(注:A,B,C顺序不同视为不同组)
考点:集合的包含关系判断及应用
专题:集合
分析:由A∩B={1,2},可知集合A,B必含元素1,2,且无其它公共元素,又由{1,2,3,4}⊆B∪C,可知3,4两个元素对于A和B两个集合的关系是相同的,5,6两个元素对于A和B两个集合的关系也是相同的,分类讨论满足条件的集合个数,最后综合讨论结果,可得答案.
解答:
解:∵A∩B={1,2},
∴集合A,B必含元素1,2,且无其它公共元素
(1)当A={1,2}时,
若3∉B,4∉B,B共有4种不同情况,那么3∈C,4∈C,C共有24=16种情况,共4×16=64种不同情况;
若3∉B,4∈B,B共有4种不同情况,那么3∈C,C共有25=32种情况,共4×32=128种不同情况;
若3∈B,4∉B,B共有4种不同情况,那么4∈C,C共有25=32种情况,共4×32=128种不同情况;
若3∈B,4∈B,B共有4种不同情况,那么3∉C,4∉C,C共有24=16种情况,共4×16=64种不同情况;
综上,共有64+128+128+64=384种不同情况;
(2)当A={1,2,3}时,则3∉B,
若4∉B,B共有4种不同情况,那么3∈C,4∈C,C共有24=16种情况,共4×16=64种不同情况;
若4∈B,B共有4种不同情况,那么3∈C,4∉C,C共有24=16种情况,共4×16=64种不同情况;
综上,共有64+64=128种不同情况;
(3)当A={1,2,4}时,由(2)可知共有128种不同情况;
(4)当A={1,2,5}时,则5∉B,
若3∉B,4∉B,B共有2种不同情况,那么3∈C,4∈C,C共有24=16种情况,共2×16=32种不同情况;
若3∉B,4∈B,B共有2种不同情况,那么3∈C,C共有25=32种情况,共2×32=64种不同情况;
若3∈B,4∉B,B共有2种不同情况,那么4∈C,C共有25=32种情况,共2×32=64种不同情况;
若3∈B,4∈B,B共有2种不同情况,那么3∉C,4∉C,C共有24=16种情况,共2×16=32种不同情况;
综上,共有32+64+64+32=192种不同情况;
(5)当A={1,2,6}时,由(4)可知共有192种不同情况;
(6)当A={1,2,3,4}时,则3∉B,4∉B,
B共有4种不同情况,那么3∈C,4∈C,C共有24=16种情况,共4×16=64种不同情况;
(7)当A={1,2,3,5}时,则3∉B,5∉B,
若4∉B,B共有2种不同情况,那么3∈C,4∈C,C共有24=16种情况,共2×16=32种不同情况;
若4∈B,B共有2种不同情况,那么3∈C,4∉C,C共有24=16种情况,共2×16=32种不同情况;
综上,共有32+32=64种不同情况;
(8)当A={1,2,3,6}时,由(7)可知共有64种不同情况;
(9)当A={1,2,4,5}时,由(7)可知共有64种不同情况;
(10)当A={1,2,4,6}时,由(7)可知共有64种不同情况;
(11)当A={1,2,5,6}时,则5∉B,6∉B,
若3∉B,4∉B,B共有1种不同情况,那么3∈C,4∈C,C共有24=16种情况,共1×16=16种不同情况;
若3∉B,4∈B,B共有1种不同情况,那么3∈C,C共有25=32种情况,共1×32=32种不同情况;
若3∈B,4∉B,B共有1种不同情况,那么4∈C,C共有25=32种情况,共1×32=32种不同情况;
若3∈B,4∈B,B共有1种不同情况,那么3∉C,4∉C,C共有24=16种情况,共1×16=16种不同情况;
综上,共有16+32+32+16=96种不同情况;
(12)当A={1,2,3,4,5}时,则3∉B,4∉B,5∉B
B共有2种不同情况,那么3∈C,4∈C,C共有24=16种情况,共2×16=32种不同情况;
(13)当A={1,2,3,4,6}时,由(11)可知共有32种不同情况;
(14)当A={1,2,3,5,6}时,则3∉B,5∉B,6∉B
若4∉B,B共有1种不同情况,那么3∈C,4∈C,C共有24=16种情况,共16种不同情况;
若4∈B,B共有1种不同情况,那么3∈C,4∉C,C共有24=16种情况,共16种不同情况;
综上,共有16+16=32种不同情况;
(15)当A={1,2,4,5,6}时,由(13)可知共有32种不同情况;
(16)当A={1,2,3,4,5,6}时,则B={1,2},
那么3∈C,4∈C,C共有24=16种情况,共16种不同情况;
综上,符合条件的(A,B,C)共有384+128+128+192+192+64+64+64+64+64+96+32+32+32+32+16=1584种情况.
∴集合A,B必含元素1,2,且无其它公共元素
(1)当A={1,2}时,
若3∉B,4∉B,B共有4种不同情况,那么3∈C,4∈C,C共有24=16种情况,共4×16=64种不同情况;
若3∉B,4∈B,B共有4种不同情况,那么3∈C,C共有25=32种情况,共4×32=128种不同情况;
若3∈B,4∉B,B共有4种不同情况,那么4∈C,C共有25=32种情况,共4×32=128种不同情况;
若3∈B,4∈B,B共有4种不同情况,那么3∉C,4∉C,C共有24=16种情况,共4×16=64种不同情况;
综上,共有64+128+128+64=384种不同情况;
(2)当A={1,2,3}时,则3∉B,
若4∉B,B共有4种不同情况,那么3∈C,4∈C,C共有24=16种情况,共4×16=64种不同情况;
若4∈B,B共有4种不同情况,那么3∈C,4∉C,C共有24=16种情况,共4×16=64种不同情况;
综上,共有64+64=128种不同情况;
(3)当A={1,2,4}时,由(2)可知共有128种不同情况;
(4)当A={1,2,5}时,则5∉B,
若3∉B,4∉B,B共有2种不同情况,那么3∈C,4∈C,C共有24=16种情况,共2×16=32种不同情况;
若3∉B,4∈B,B共有2种不同情况,那么3∈C,C共有25=32种情况,共2×32=64种不同情况;
若3∈B,4∉B,B共有2种不同情况,那么4∈C,C共有25=32种情况,共2×32=64种不同情况;
若3∈B,4∈B,B共有2种不同情况,那么3∉C,4∉C,C共有24=16种情况,共2×16=32种不同情况;
综上,共有32+64+64+32=192种不同情况;
(5)当A={1,2,6}时,由(4)可知共有192种不同情况;
(6)当A={1,2,3,4}时,则3∉B,4∉B,
B共有4种不同情况,那么3∈C,4∈C,C共有24=16种情况,共4×16=64种不同情况;
(7)当A={1,2,3,5}时,则3∉B,5∉B,
若4∉B,B共有2种不同情况,那么3∈C,4∈C,C共有24=16种情况,共2×16=32种不同情况;
若4∈B,B共有2种不同情况,那么3∈C,4∉C,C共有24=16种情况,共2×16=32种不同情况;
综上,共有32+32=64种不同情况;
(8)当A={1,2,3,6}时,由(7)可知共有64种不同情况;
(9)当A={1,2,4,5}时,由(7)可知共有64种不同情况;
(10)当A={1,2,4,6}时,由(7)可知共有64种不同情况;
(11)当A={1,2,5,6}时,则5∉B,6∉B,
若3∉B,4∉B,B共有1种不同情况,那么3∈C,4∈C,C共有24=16种情况,共1×16=16种不同情况;
若3∉B,4∈B,B共有1种不同情况,那么3∈C,C共有25=32种情况,共1×32=32种不同情况;
若3∈B,4∉B,B共有1种不同情况,那么4∈C,C共有25=32种情况,共1×32=32种不同情况;
若3∈B,4∈B,B共有1种不同情况,那么3∉C,4∉C,C共有24=16种情况,共1×16=16种不同情况;
综上,共有16+32+32+16=96种不同情况;
(12)当A={1,2,3,4,5}时,则3∉B,4∉B,5∉B
B共有2种不同情况,那么3∈C,4∈C,C共有24=16种情况,共2×16=32种不同情况;
(13)当A={1,2,3,4,6}时,由(11)可知共有32种不同情况;
(14)当A={1,2,3,5,6}时,则3∉B,5∉B,6∉B
若4∉B,B共有1种不同情况,那么3∈C,4∈C,C共有24=16种情况,共16种不同情况;
若4∈B,B共有1种不同情况,那么3∈C,4∉C,C共有24=16种情况,共16种不同情况;
综上,共有16+16=32种不同情况;
(15)当A={1,2,4,5,6}时,由(13)可知共有32种不同情况;
(16)当A={1,2,3,4,5,6}时,则B={1,2},
那么3∈C,4∈C,C共有24=16种情况,共16种不同情况;
综上,符合条件的(A,B,C)共有384+128+128+192+192+64+64+64+64+64+96+32+32+32+32+16=1584种情况.
点评:本题考查的知识点是满足条件的集合个数,当集合中不确定元素为n个时,满足条件的集合共有2n个.

练习册系列答案
相关题目
在△ABC中,已知sin2A+sin2B+sin2C=2,则△ABC为( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
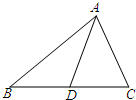 如图,已知△ABC中,∠BAD=30°,∠CAD=45°,AB=3,AC=2,则
如图,已知△ABC中,∠BAD=30°,∠CAD=45°,AB=3,AC=2,则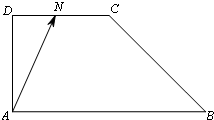 如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=
如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=