题目内容
设直线l过椭圆
+y2=1的右焦点,与椭圆相交于A、B两点,O是坐标原点,当△OAB的面积最大时,求直线l的方程.
| x2 |
| 4 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:椭圆
+y2=1的右焦点为(
,0),则设l:x=my+
,代入椭圆
+y2=1,整理,利用韦达定理,根据S△OAB=
•
•|y1-y2|,再利用换元法,结合基本不等式,即可得出结论.
| x2 |
| 4 |
| 3 |
| 3 |
| x2 |
| 4 |
| 1 |
| 2 |
| 3 |
解答:
解:椭圆
+y2=1的右焦点为(
,0),则设l:x=my+
,
代入椭圆
+y2=1,整理可得(m2+4)y2+2
my-1=0,
设A(x1,y1)、B(x2,y2),则y1+y2=-
,y1y2=-
,
∴|y1-y2|=
=
,
∴S△OAB=
•
•|y1-y2|=
•
令
=t(t≥1),则S△OAB=2
•
=2
•
≤1,
当且仅当t=
,即t=
时,△OAB的面积最大,
此时m=±
,直线l的方程为x=±
y+
.
| x2 |
| 4 |
| 3 |
| 3 |
代入椭圆
| x2 |
| 4 |
| 3 |
设A(x1,y1)、B(x2,y2),则y1+y2=-
2
| ||
| m2+4 |
| 1 |
| m2+4 |
∴|y1-y2|=
| (y1+y2)2-4y1y2 |
4
| ||
| m2+4 |
∴S△OAB=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
4
| ||
| m2+4 |
令
| m2+1 |
| 3 |
| t |
| t2+3 |
| 3 |
| 1 | ||
t+
|
当且仅当t=
| 3 |
| t |
| 3 |
此时m=±
| 2 |
| 2 |
| 3 |
点评:本题考查椭圆的性质,考查直线与椭圆的位置关系,考查韦达定理的运用,正确表示△OAB的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
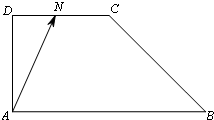 如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=
如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=