题目内容
19.在极坐标系中,点A和点B的极坐标分别为(2,$\frac{π}{3}$),(3,0),O为极点,求:(1)|AB|;
(2)求△AOB的面积.
分析 (1)利用余弦定理即可得出.
(2)利用三角形面积计算公式即可得出.
解答 解:(1)△AOB中,|OA|=2,|OB|=3,∠AOB=$\frac{π}{3}$由余弦定理得
|AB|=$\sqrt{{2}^{2}+{3}^{2}-2×2×3cos\frac{π}{3}}$=$\sqrt{7}$.
(2)S△AOB=$\frac{1}{2}$|OA|•|OB|•sin∠AOB=$\frac{1}{2}$×2×3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了极坐标的应用、余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.设X~B(4,p),其中0<p<$\frac{1}{2}$,且P(X=2)=$\frac{8}{27}$,那么P(X=1)=( )
| A. | $\frac{8}{81}$ | B. | $\frac{16}{81}$ | C. | $\frac{8}{27}$ | D. | $\frac{32}{81}$ |
7.设集合An={1,2,3,…,n}(n∈N*,n≥3),记An中的元素组成的非空子集为$A_i^'$(i∈N*,i=1,2,3,…,2n-1),对于?i∈{1,2,3,…,2n-1},$A_i^'$中的最小元素和为Sn,则S5=( )
| A. | 32 | B. | 57 | C. | 75 | D. | 480 |
11.函数f(x)的图象如图所示,则下列关系正确的是( )
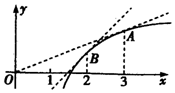

| A. | 0<f'(2)<f'(3)<f(3)-f(2) | B. | 0<f'(2)<f(3)-f(2)<f'(3) | C. | 0<f'(3)<f(3)-f(2)<f'(2) | D. | 0<f(3)-f(2)<f'(2)-f'(3) |
9.已知数列{an}中,a3=2,a6=1,若{ $\frac{1}{1+{a}_{n}}$ }是等差数列,则a11等于( )
| A. | 0 | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |