题目内容
7.设集合An={1,2,3,…,n}(n∈N*,n≥3),记An中的元素组成的非空子集为$A_i^'$(i∈N*,i=1,2,3,…,2n-1),对于?i∈{1,2,3,…,2n-1},$A_i^'$中的最小元素和为Sn,则S5=( )| A. | 32 | B. | 57 | C. | 75 | D. | 480 |
分析 题意得:在所有非空子集中每个元素出现2n-1次.故有2n-1个子集含1,有2n-2个子集不含1含2,有2n-3子集不含1,2,含3…有2i-1个子集不含1,2,3…i-1,而含i,进而利用错位相减法求出其和.
解答 解:由题意得:在所有非空子集中每个元素出现2n-1次.
故有2n-1个子集含1,有2n-2个子集不含1含2,有2n-3子集不含1,2,含3…有2i-1个子集不含1,2,3…i-1,而含i.
所以Sn=2n-1×1+2n-2×2+…+21×(n-1)+n
Sn=n•1+(n-1)•2+…+2•2n-2+1•2n-1…①
所以2Sn=n•2+(n-1)•4+…+2•2n-1+1•2n…②
所以①-②可得-Sn=n-(2+4+…+2n-1+2n)
所以Sn=2n+1-n-2
所以S5=26-5-2=57.
故选:B
点评 本题考查了错位相减法、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
15.设定点F1(0,2),F2(0,-2),动点P满足条件$|{P{F_1}}|+|{P{F_2}}|=a+\frac{4}{a}(a>0)$,则点P的轨迹是( )
| A. | 椭圆 | B. | 线段 | C. | 不存在 | D. | 椭圆或线段 |
2.学校对同时从高一,高二,高三三个不同年级的某些学生进行抽样调查,从各年级抽出人数如表所示.工作人员用分层抽样的方法从这些学生中共抽取6人进行调查
(1)求这6位学生来自高一,高二,高三各年级的数量;
(2)若从这6位学生中随机抽取2人再做进一步的调查,求这2人来自同一年级的概率.
| 年级 | 高一 | 高二 | 高三 |
| 数量 | 50 | 150 | 100 |
(2)若从这6位学生中随机抽取2人再做进一步的调查,求这2人来自同一年级的概率.
17.已知sin(α+$\frac{π}{3}$)=-$\frac{1}{2}$,α∈(0,π),则cosα=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
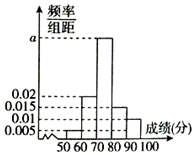 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.