题目内容
11．函数f（x）的图象如图所示，则下列关系正确的是（ ）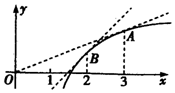
| A． | 0＜f'（2）＜f'（3）＜f（3）-f（2） | B． | 0＜f'（2）＜f（3）-f（2）＜f'（3） | C． | 0＜f'（3）＜f（3）-f（2）＜f'（2） | D． | 0＜f（3）-f（2）＜f'（2）-f'（3） |
分析 由题意已知函数f（x）的图象，先判断它的单调性，然后根据函数图象斜率的变化，判断f（x）′的增减性，最后根据函数的凸凹性进行判断，从而求解．
解答 解：由函数f（x）的图象可知：
当x≥0时，f（x）单调递增，且当x=0时，f（0）＜0，
∴f′（2），f′（3），f（3）-f（2）＞0，
由此可知f′（x）＞0，
∵直线的斜率逐渐减小，
∴f′（x）单调递减，
∴f′（2）＞f′（3），
∵f（x）为凸函数，
∴f（3）-f（2）＜f′（2）
∴0＜f′（3）＜f（3）-f（2）＜f′（2），
故选C．
点评 此题主要考查函数导数与函数单调性之间的关系，掌握并会熟练运用导数与函数单调性的关系，另外还考查学生的读图能力，要善于从图中获取信息．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
2．学校对同时从高一，高二，高三三个不同年级的某些学生进行抽样调查，从各年级抽出人数如表所示．工作人员用分层抽样的方法从这些学生中共抽取6人进行调查
（1）求这6位学生来自高一，高二，高三各年级的数量；
（2）若从这6位学生中随机抽取2人再做进一步的调查，求这2人来自同一年级的概率．
| 年级 | 高一 | 高二 | 高三 |
| 数量 | 50 | 150 | 100 |
（2）若从这6位学生中随机抽取2人再做进一步的调查，求这2人来自同一年级的概率．
6．一个总体分为A，B，C三层，用分层抽样方法从总体中抽取容量为50的样本，已知B层中每个个体被抽到的概率都为$\frac{1}{12}$，则总体容量为（ ）
| A． | 150 | B． | 200 | C． | 500 | D． | 600 |
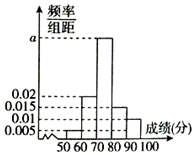为了了解某学校高二年级学生的物理成绩，从中抽取n名学生的物理成绩（百分制）作为样本，按成绩分成5组：[50，60），[60，70），[70，80），[80，90），[90，100]，频率分布直方图如图所示，成绩落在[70，80）中的人数为20．
3．函数f（x）=x2+2x+1的单调递增区间是（ ）
| A． | [-1，+∞） | B． | [1，+∞） | C． | （-∞，-1] | D． | （-∞，1] |
20．在△ABC中，c=$\sqrt{3}$，B=45°，C=60°，则b=（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $\sqrt{2}$ |