有6个零件.其中4个一等品.2个二等品.若从这6个零件中任意取2个.那么至少有1个一等品的概率是$\frac{14}{15}$．题目和参考答案——青夏教育精英家教网——

题目内容

4．有6个零件，其中4个一等品，2个二等品，若从这6个零件中任意取2个，那么至少有1个一等品的概率是$\frac{14}{15}$．

分析至少有1个一等品的对立事件是2个都是二等品，由此利用对立事件概率计算公式能求出至少有1个一等品的概率．

解答解：有6个零件，其中4个一等品，2个二等品，从这6个零件中任意取2个，
基本事件总数n=${C}_{6}^{2}=15$，
至少有1个一等品的对立事件是2个都是二等品，
∴至少有1个一等品的概率是p=1-$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}$=$\frac{14}{15}$．
故答案为：$\frac{14}{15}$．

点评本题考查概率、对立事件概率计算公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．

练习册系列答案

寒假作业快乐假期新疆青少年出版社系列答案

寒假作业阳光出版社系列答案

新锐图书假期园地寒假作业系列答案

假期作业青海人民出版社系列答案

衔接教材学期复习寒假吉林教育出版社系列答案

书香天博寒假作业西安出版社系列答案

智趣寒假温故知新系列答案

桂壮红皮书假期生活寒假作业系列答案

和谐假期云南科技出版社系列答案

快乐寒假广西师范大学出版社系列答案

相关题目

14．复数z=（m²-2m-3）+（m²-4m+3）i是纯虚数，实数m=（　　）

15．设定点F₁（0，2），F₂（0，-2），动点P满足条件$|{P{F_1}}|+|{P{F_2}}|=a+\frac{4}{a}（a＞0）$，则点P的轨迹是（　　）

椭圆或线段

12．2017²⁰¹⁶除以2018的余数为1．

19．在极坐标系中，点A和点B的极坐标分别为（2，$\frac{π}{3}$），（3，0），O为极点，求：
（1）|AB|；
（2）求△AOB的面积．

9．已知函数f（x）=sinx，g（x）=e^x•f'（x），其中e为自然对数的底数．
（1）求曲线y=g（x）在点（0，g（0））处的切线方程；
（2）若对任意$x∈[{-\frac{π}{2}，0}]$，不等式g（x）≥x•f（x）+m恒成立，求实数m的取值范围；
（3）试探究当$x∈[{\frac{π}{4}，\frac{π}{2}}]$时，方程g（x）=x•f（x）的解的个数，并说明理由．

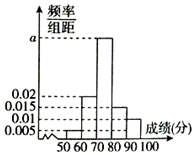为了了解某学校高二年级学生的物理成绩，从中抽取n名学生的物理成绩（百分制）作为样本，按成绩分成5组：[50，60），[60，70），[70，80），[80，90），[90，100]，频率分布直方图如图所示，成绩落在[70，80）中的人数为20．
（1）求a和n的值；
（2）根据样本估计总体的思想，估计该校高二学生物理成绩的平均数$\overline x$和中位数m；
（3）成绩在80分以上（含80分）为优秀，样本中成绩落在[50，80）中的男、女人数比为1：2，成绩落在[80，100]中的男、女生人数比为3：2，完成下列表格．

	男生	女生	合计
优秀
不优秀
合计

13．设P在[0，5]上随机取值，求方程x²+px+1=0有实根的概率为（　　）

14．在△ABC中，角A、B、C所对的边分别是a、b、c，若$a=\sqrt{6}$，b=2，A=60°，则B=（　　）