题目内容
8.设函数f(x)=sinxcosx-$\sqrt{3}$cos(x+π)cosx(x∈R).(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若函数y=f(x)的图象按$\overrightarrow{b}$=($\frac{π}{4}$,$\frac{\sqrt{3}}{2}$)平移后得到函数y=g(x)的图象,求y=g(x)在[0,$\frac{π}{4}$]上的最大值.
分析 (Ⅰ)利用二倍角公式以及两角和与差三角函数化简函数的表达式,然后求解f(x)的最小正周期;
(Ⅱ)利用函数的图象的平移变换求出新函数的解析式,然后求解相位的范围,利用正弦函数的有界性求解函数的最值即可.
解答 解:(Ⅰ)函数f(x)=sinxcosx-$\sqrt{3}$cos(x+π)cosx
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x+$\frac{\sqrt{3}}{2}$
=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$.
$f(x)=sin(2x+\frac{π}{3})+\frac{{\sqrt{3}}}{2}$,所以函数f(x)的最小正周期为π;
(Ⅱ)函数y=f(x)的图象按$\overrightarrow{b}$=($\frac{π}{4}$,$\frac{\sqrt{3}}{2}$)平移后得到函数y=g(x)的图象,
可得$g(x)=f(x-\frac{π}{4})+\frac{{\sqrt{3}}}{2}=sin(2x-\frac{π}{6})+\sqrt{3}$.
由$x∈[0,\frac{π}{4}]⇒2x-\frac{π}{6}∈[-\frac{π}{6},\frac{π}{3}]$,g(x)为增函数,
所以g(x)在$[0,\frac{π}{4}]$上的最大值为$g(\frac{π}{4})=\frac{{3\sqrt{3}}}{2}$.
点评 本题考查两角和与差的三角函数,二倍角公式的应用,考查计算能力.

练习册系列答案
相关题目
3.函数f(x)=x2+2x+1的单调递增区间是( )
| A. | [-1,+∞) | B. | [1,+∞) | C. | (-∞,-1] | D. | (-∞,1] |
13.设P在[0,5]上随机取值,求方程x2+px+1=0有实根的概率为( )
| A. | 0.2 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
20.在△ABC中,c=$\sqrt{3}$,B=45°,C=60°,则b=( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
17.已知sin(α+$\frac{π}{3}$)=-$\frac{1}{2}$,α∈(0,π),则cosα=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
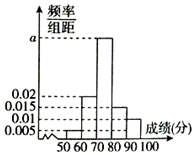 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.