题目内容
13.利用单位圆,求使下列不等式成立的x的范围(1)cosx≥$\frac{\sqrt{2}}{2}$
(2)tanx≤1
(3)sinx≤-$\frac{1}{2}$.
分析 由已知条件作出单位圆,利用单位圆求出在[0,2π)内满足条件的x的范围,再利用终边相同的角的概念,即可求出符合条件的角x的范围.
解答 解:(1)∵cosx≥$\frac{\sqrt{2}}{2}$,作出单位图,如图①所示:
结合单位圆,得-$\frac{π}{4}$≤α≤$\frac{π}{4}$,
∴cosx≥$\frac{\sqrt{2}}{2}$的x的范围是{x|-$\frac{π}{4}$+2kπ≤x≤$\frac{π}{4}$+2kπ,k∈Z};
(2)∵tanx≤1,
作出单位图,如图②所示:
结合单位圆,得α≤$\frac{π}{4}$,
∴符合tanx≤1的角x的范围是{x|-$\frac{π}{2}$+kπ<x≤$\frac{π}{4}$+kπ,k∈Z}:
(3)∵sinx≤-$\frac{1}{2}$,
∴作出单位图,如图③所示: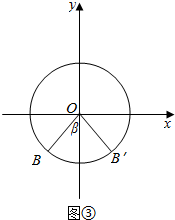
结合单位圆,得$\frac{5π}{4}$≤β≤$\frac{7π}{4}$,
∴符合sinx≤-$\frac{1}{2}$的x的范围是{x|$\frac{5π}{4}$+2kπ≤x≤$\frac{7π}{4}$+2kπ,k∈Z}.
点评 本题考查了利用单位圆求满足条件的角的取值范围的应用问题,解题时要认真审题,注意单位圆的性质的合理运用,是基础题目.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
3.设函数f(x)=|3x-1|,c<b<a,且f(c)>f(a)>f(b),则下列关系中一定成立的是( )
| A. | 3c+3a=2 | B. | 3c+3a>2 | ||
| C. | 3c+3a<2 | D. | 3c+3a与2的大小关系不确定 |
18.下列函数中,既是偶函数,周期为π的是( )
| A. | y=sin|x| | B. | y=|tanx| | C. | y=|sin2x| | D. | y=cos(2x+$\frac{x}{2}$) |
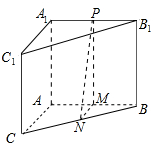 在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.
在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.