题目内容
3.设函数f(x)=|3x-1|,c<b<a,且f(c)>f(a)>f(b),则下列关系中一定成立的是( )| A. | 3c+3a=2 | B. | 3c+3a>2 | ||
| C. | 3c+3a<2 | D. | 3c+3a与2的大小关系不确定 |
分析 运用分段函数的形式写出f(x)的解析式,作出f(x)=|3x-1|的图象,由题意可得c<0,a>0,3c<1且3a>1,且f(c)-f(a)>0,去掉绝对值,化简即可得到结论.
解答  解:f(x)=|3x-1|=$\left\{\begin{array}{l}{{3}^{x}-1,x≥0}\\{1-{3}^{x},x<0}\end{array}\right.$,
解:f(x)=|3x-1|=$\left\{\begin{array}{l}{{3}^{x}-1,x≥0}\\{1-{3}^{x},x<0}\end{array}\right.$,
作出f(x)=|3x-1|的图象如图所示,
由图可知,要使c<b<a且f(c)>f(a)>f(b)成立,
则有c<0且a>0,
故必有3c<1且3a>1,
又f(c)-f(a)>0即为1-3c-(3a-1)>0,
所以3c+3a<2.
故选C.
点评 本题考点是指数函数单调性的应用,考查用指数函数单调性确定参数的范围,本题借助函数图象来辅助研究,由图象辅助研究函数性质是函数图象的重要作用,以形助数的解题技巧必须掌握.

练习册系列答案
相关题目
14.哈尔滨市投资修建冰雪大世界,为了调查此次修建冰雪大世界能否收回成本,组委会成立了一个调查小组对国内参观冰雪大世界的游客的消费指数(单位:百元)进行调查,在调查的1000位游客中有100位哈尔滨本地游客,把哈尔滨本地游客记为A组,内外地游客记为B组,按分层抽样从这1000人中抽取A,B组人数如下表:
A组:
B组:
(1)确定a的值,再分别在答题纸上完成A组与B组的频率分布直方图;
(2)分别估计A,B两组游客消费指数的平均数,并估计被调查的1000名游客消费指数的平均数.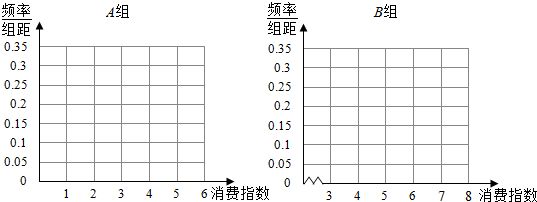
A组:
| 消费指数(百元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
| 人数 | 3 | 4 | 6 | 5 | 2 |
| 消费指数(百元) | [3,4) | [4,5) | [5,6) | [6,7) | [7,8] |
| 人数 | 9 | 36 | a | 54 | 9 |
(2)分别估计A,B两组游客消费指数的平均数,并估计被调查的1000名游客消费指数的平均数.

8.在长方体ABCD-A1B1C1D1中,AB=6,BC=4,AA1=2,P,Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为( )
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{34}$ | D. | 5$\sqrt{2}$ |
15.已知实数a,b满足2a2-5lna-b=0,c∈R,则$\sqrt{(a-c)^{2}+(b+c)^{2}}$的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{9}{2}$ |
12.设F1、F2是双曲线x2-$\frac{{y}^{2}}{4}$=1的左、右两个焦点,在双曲线右支上取一点P,使|OP|=|PF2|(O为坐标原点)且|PF1|=λ|PF2|,则实数λ的值为( )
| A. | $\frac{7}{3}$ | B. | 2或$\frac{1}{2}$ | C. | 3 | D. | 2 |
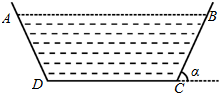 2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?
2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?