Question

1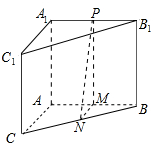．在三棱锥ABC-A₁B₁C₁中，∠BAC=90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边的长为1的等腰直角三角形，设点M，N，P分别是棱AB，BC，B₁C₁的中点．
（1）证明：A₁B₁⊥平面PMN；
（2）求三棱锥P-A₁MN的体积．

Answer 1

分析 （1）根据三视图得出三棱柱的结构特征，利用中位线定理得出MN⊥A₁B₁，PM⊥A₁B₁，从而得出A₁B₁⊥平面PMN；
（2）V${\;}_{棱锥P-{A}_{1}MN}$=V${\;}_{棱锥{A}_{1}-PMN}$=$\frac{1}{3}$•S_△PMN•A₁P．

解答 解：（1）∵三棱柱的正视图和侧视图是边长为1正方形，俯视图是直角边的长为1的等腰直角三角形，
∴三棱柱ABC-A₁B₁C₁是直三棱柱，AB=AC=AA₁=1，AB⊥AC，
∵点M，N，P分别是棱AB，BC，B₁C₁的中点．
∴MN⊥AB，A₁B₁⊥PM，∵A₁B₁∥AB，
∴A₁B₁⊥MN，∵PM∩MN=M，PM?平面PMN，MN?平面PMN，
∴A₁B₁⊥平面PMN．
（2）连结A₁M，A₁N，
∵PM∥A₁A，MN∥AC，∴∠PMN=∠A₁AC=90°，
∴V${\;}_{棱锥P-{A}_{1}MN}$=V${\;}_{棱锥{A}_{1}-PMN}$=$\frac{1}{3}$•S_△PMN•A₁P=$\frac{1}{3}×\frac{1}{2}×PM×MN×{A}_{1}P$=$\frac{1}{3}×\frac{1}{2}×1×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{24}$．

点评 本题考查了空间几何体的三视图，线面垂直的判定，三棱锥的体积计算，是中档题．