题目内容
已知椭圆
+
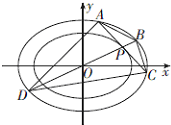
=1(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(1)当p+q≤0时,求椭圆的离心率的取值范围;
(2)若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时,(
+
).
的最小值为
,求椭圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)当p+q≤0时,求椭圆的离心率的取值范围;
(2)若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时,(
| MF |
| OD |
| MO |
| 7 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:向量与圆锥曲线
分析:(1)求出线段AF、AB的垂直平分线方程,联立求得圆心坐标,由p+q≤0得到关于a,b,c的关系式,结合b2=a2-c2可得椭圆的离心率的取值范围;
(2)当椭圆离心率取得最小值
时,把a,b用含c的代数式表示,代入椭圆方程,设出M点坐标,求出(
+
)•
,然后对c分类求出最小值,然后由最小值等于
求得c的值,则椭圆方程可求.
(2)当椭圆离心率取得最小值
| ||
| 2 |
| MF |
| OD |
| MO |
| 7 |
| 2 |
解答:
解:(1)设半焦距为c.
由题意AF、AB的中垂线方程分别为x=
,y-
=
(x-
),
联立
,解得
.
于是圆心坐标为(
,
).
由p+q=
+
≤0,
整理得ab-bc+b2-ac≤0,
即(a+b)(b-c)≤0,
∴b≤c,于是b2≤c2,即a2=b2+c2≤2c2.
∴e2=
≥
,即
≤e<1;
(2)当e=
时,a=
b=
c,此时椭圆的方程为
+
=1,
设M(x,y),则-
c≤x≤
c,
∴(
+
)•
=
x2-x+c2=
(x-c)2+c2-
.
当c≥
时,上式的最小值为c2-
,即c2-
=
,得c=2;
当0<c<
时,上式的最小值为
(
c)2-
c+c2,即
(
c)2-
c+c2=
,
解得c=
,不合题意,舍去.
综上所述,椭圆的方程为
+
=1.
由题意AF、AB的中垂线方程分别为x=
| a-c |
| 2 |
| b |
| 2 |
| a |
| b |
| a |
| 2 |
联立
|
|
于是圆心坐标为(
| a-c |
| 2 |
| b2-ac |
| 2b |
由p+q=
| a-c |
| 2 |
| b2-ac |
| 2b |
整理得ab-bc+b2-ac≤0,
即(a+b)(b-c)≤0,
∴b≤c,于是b2≤c2,即a2=b2+c2≤2c2.
∴e2=
| c2 |
| a2 |
| 1 |
| 2 |
| ||
| 2 |
(2)当e=
| ||
| 2 |
| 2 |
| 2 |
| x2 |
| 2c2 |
| y2 |
| c2 |
设M(x,y),则-
| 2 |
| 2 |
∴(
| MF |
| OD |
| MO |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当c≥
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
当0<c<
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 7 |
| 2 |
解得c=
| ||||
| 4 |
综上所述,椭圆的方程为
| x2 |
| 8 |
| y2 |
| 4 |
点评:本题考查直线与椭圆的位置关系的应用,考查与向量有关的最值问题,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是高考试卷中的压轴题.

练习册系列答案
相关题目
从2、3、5、7这四个质数中任取两个相乘,可以得到不相等的积的个数是( )
| A、4 | B、5 | C、6 | D、8 |
 已知曲线C1:
已知曲线C1: