题目内容
 已知曲线C1:
已知曲线C1:| x2 |
| 4 |
| y2 |
| 4λ |
| x2 |
| 4λ |
| y2 |
| 4λ2 |
(1)求λ的值;
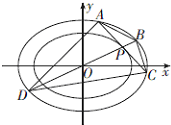
(2)设P(x0,y0)为曲线C2上一点,过点P作直线交曲线C1于A,C两点,直线OP交曲线C1于B,D两点,若P为AC中点.
①求证:直线AC的方程为x0x+2y0y=2;
②四边形ABCD的面积是否为定值?若是,请求出该定值;若不是,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用曲线C2的左顶点恰为曲线C1的左焦点,可得
=
,从而可求λ的值;
(2)①先求出AC的斜率,可得AC的方程,从而可得结论;
②AC的方程与椭圆方程联立,求出|AC|,再求出B,D到直线AC的距离,即可得出结论.
| 4λ |
| 4-4λ |
(2)①先求出AC的斜率,可得AC的方程,从而可得结论;
②AC的方程与椭圆方程联立,求出|AC|,再求出B,D到直线AC的距离,即可得出结论.
解答:
(1)解:∵曲线C2的左顶点恰为曲线C1的左焦点,
∴
=
,
∴λ=
;
(2)①证明:由题意,B(
x0,
y0),D(-
x0,-
y0),
∴kOP•kAC=-
=-
,
∴kAC=-
,
∴AC的方程为y-y0=-
(x-x0),即x0x+2y0y=2,
y0=0时,x0=±
满足x0x+2y0y=2;
②解:AC的方程与椭圆方程联立,可得(1+
)x2-
x+
-4=0,即2x2-4x0x+4-8y2=0,
∴|AC|=
|xA-xC|=
,
B,D到直线AC的距离d1=
,d2=
∴S=
|AC|(d1+d2)=
•(
+
)=4
当y0=0时,ABCD的面积也为4,
∴四边形ABCD的面积为定值4.
∴
| 4λ |
| 4-4λ |
∴λ=
| 1 |
| 2 |
(2)①证明:由题意,B(
| 2 |
| 2 |
| 2 |
| 2 |
∴kOP•kAC=-
| 4λ |
| 4 |
| 1 |
| 2 |
∴kAC=-
| x0 |
| 2y0 |
∴AC的方程为y-y0=-
| x0 |
| 2y0 |
y0=0时,x0=±
| 2 |
②解:AC的方程与椭圆方程联立,可得(1+
| x02 |
| 2y02 |
| 2x0 |
| y02 |
| 2 |
| y02 |
∴|AC|=
1+
|
1+
|
| 8y02 |
B,D到直线AC的距离d1=
2
| ||
|
2
| ||
|
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
1+
|
| 8y02 |
2
| ||
|
2
| ||
|
当y0=0时,ABCD的面积也为4,
∴四边形ABCD的面积为定值4.
点评:本题考查直线与椭圆的位置关系,考查弦长的计算,考查面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
实数x,y满足
,若z=kx+y的最大值为13,则实数k=( )
|
| A、2 | ||
B、
| ||
C、
| ||
| D、5 |
 如图,已知椭圆C:
如图,已知椭圆C: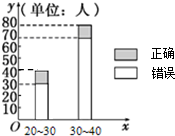 “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.