题目内容
已知函数f(x)=|x-2|-a.
(1)当a=1时,求f(x)≤1的解集;
(2)若f(x)≥|x+3|恒成立,求a的取值范围.
(1)当a=1时,求f(x)≤1的解集;
(2)若f(x)≥|x+3|恒成立,求a的取值范围.
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:(1)当a=1时,解不等式|x-2|-1≤1即可求得其解集;
(2))|x-2|-a≥|x+3|恒成立?a≤|x-2|-|x+3|恒成立,令g(x)=|x-2|-|x+3|,则a≤g(x)min,求得g(x)min即可.
(2))|x-2|-a≥|x+3|恒成立?a≤|x-2|-|x+3|恒成立,令g(x)=|x-2|-|x+3|,则a≤g(x)min,求得g(x)min即可.
解答:
解:(1)当a=1时,f(x)≤1?|x-2|-1≤1,
∴|x-2|≤2,
解得:0≤x≤4.
∴当a=1时,f(x)≤1的解集为{x|0≤x≤4};
(2)∵|x-2|-a≥|x+3|恒成立,
∴a≤|x-2|-|x+3|恒成立,
令g(x)=|x-2|-|x+3|,
则a≤g(x)min,
当x<-3时,g(x)=5;
当-3≤x≤2时,g(x)=-2x-1∈[-5,5];
当x>3时,g(x)=-5;
∴g(x)min=-5.
∴a≤-5,
即a的取值范围为(-∞,-5].
∴|x-2|≤2,
解得:0≤x≤4.
∴当a=1时,f(x)≤1的解集为{x|0≤x≤4};
(2)∵|x-2|-a≥|x+3|恒成立,
∴a≤|x-2|-|x+3|恒成立,
令g(x)=|x-2|-|x+3|,
则a≤g(x)min,
当x<-3时,g(x)=5;
当-3≤x≤2时,g(x)=-2x-1∈[-5,5];
当x>3时,g(x)=-5;
∴g(x)min=-5.
∴a≤-5,
即a的取值范围为(-∞,-5].
点评:本题考查绝对值不等式的解法,着重考查分类讨论思想、构造函数思想与函数恒成立问题,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
若直线l1:x+ay-1=0与l2:4x-2y+3=0垂直,则二项式(ax2-
)5展开式中x的系数为( )
| 1 |
| x |
| A、-40 | B、-10 |
| C、10 | D、40 |
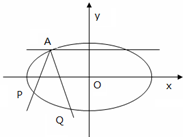 如图,焦点在x轴的椭圆,离心率e=
如图,焦点在x轴的椭圆,离心率e= 如图所示,f(x)是定义在区间[-c,c](c>0)上的奇函数,令g(x)=af(x)+b,并有关于函数g(x)的四个论断:
如图所示,f(x)是定义在区间[-c,c](c>0)上的奇函数,令g(x)=af(x)+b,并有关于函数g(x)的四个论断: