题目内容
若数列{an}的前n项和为Sn,对任意正整数n都有6Sn=1-2an,记bn=log
an.
(1)求数列{bn}的通项公式;
(2)若cn+1-cn=bn,c1=0,求证:对任意n≥2,n∈N*都有
+
+…+
<
.
| 1 |
| 2 |
(1)求数列{bn}的通项公式;
(2)若cn+1-cn=bn,c1=0,求证:对任意n≥2,n∈N*都有
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 3 |
| 4 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由6Sn=1-2an,求出6Sn-1=1-2an-1,两式相减推导出数列{an}是首项a1=
,公比q=
的等比数列,由此利用记bn=log
an,能求出数列{bn}的通项公式.
(2)由cn+1-cn=bn=2n+1,利用累加法能求出cn=(n-1)(n+1),由此能证明
+
+…+
<
对任意n≥2,n∈N*均成立.
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 2 |
(2)由cn+1-cn=bn=2n+1,利用累加法能求出cn=(n-1)(n+1),由此能证明
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 3 |
| 4 |
解答:
解:(1)由6S1=1-2a1,得6a1=1-2a1,解得a1=
.
由6Sn=1-2an①,
当n≥2时,有6Sn-1=1-2an-1②,
①-②得:
=
,
∴数列{an}是首项a1=
,公比q=
的等比数列,
∴an=a1qn-1=
×(
)n-1=(
)2n+1,
∴bn=log
an=log
(
)2n+1=2n+1.
(2)∵cn+1-cn=bn=2n+1,
∴cn-cn-1=bn-1=2(n-1)+1,
cn-1-cn-2=bn-2=2(n-2)+1,
…,
c3-c2=b2=2×2+1,
c2-c1=b1=2×1+1,
以上n-1个式子相加得:
cn-c1=bn-1=2(1+2+3+…+n-1)+n-1=n2-1,
∴cn=(n-1)(n+1),
∴
=
=
(
-
),
∴
+
+…+
=
(1-
+
-
+
-
+…+
-
+
-
)
=
(1+
-
-
)=
-
(
+
),
∵
(
+
)>0,
∴
+
+…+
<
对任意n≥2,n∈N*均成立.
| 1 |
| 8 |
由6Sn=1-2an①,
当n≥2时,有6Sn-1=1-2an-1②,
①-②得:
| an |
| an-1 |
| 1 |
| 4 |
∴数列{an}是首项a1=
| 1 |
| 8 |
| 1 |
| 4 |
∴an=a1qn-1=
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 2 |
∴bn=log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵cn+1-cn=bn=2n+1,
∴cn-cn-1=bn-1=2(n-1)+1,
cn-1-cn-2=bn-2=2(n-2)+1,
…,
c3-c2=b2=2×2+1,
c2-c1=b1=2×1+1,
以上n-1个式子相加得:
cn-c1=bn-1=2(1+2+3+…+n-1)+n-1=n2-1,
∴cn=(n-1)(n+1),
∴
| 1 |
| cn |
| 1 |
| (n-1)(n+1) |
| 1 |
| 2 |
| 1 |
| n-1 |
| 1 |
| n+1 |
∴
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-2 |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n+1 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∵
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 3 |
| 4 |
点评:本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意累加法和裂项求和法的合理运用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
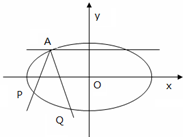 如图,焦点在x轴的椭圆,离心率e=
如图,焦点在x轴的椭圆,离心率e=