题目内容
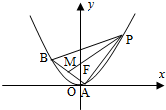 已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,
已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,| PF |
| FM |
(Ⅰ)若|PF|=3,求点M的坐标;
(Ⅱ)求△ABP面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(Ⅰ)根据抛物线的定义,利用条件|PF|=3,求建立方程关系即可求点M的坐标;
(Ⅱ)设直线AB的方程为y=kx+m,利用直线和抛物线联立结合弦长公式公式以及点到直线的距离公式,利用导数即可求出三角形面积的最值.
(Ⅱ)设直线AB的方程为y=kx+m,利用直线和抛物线联立结合弦长公式公式以及点到直线的距离公式,利用导数即可求出三角形面积的最值.
解答:
解:(Ⅰ)由题意知焦点F(0,1),准线方程为y=-1,
设P(x0,y0),由抛物线的定义可知|PF|=y0+1,解得y0=2,
∴x0=±2
,即P(2
,2)或P(-2
,2),
由
=3
,得M(-
,
)或M(
,
).
(Ⅱ)设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
由
得x2-4kx-4m=0,
于是△=16k2+16m>0,x1+x2=4k,x1x2=-4m,
即AB的中点M的坐标为(2k,2k2+m)
由
=3
,得(-x0,1-y0)=3(2k,2k2+m-1),
解得
,由
=4y0,得k2=-
m+
,
由△>0,k>0得-
<m≤
,
又∵|AB|=4
•
,
点F到直线AB的距离d=
,
∴S△ABP=4S△ABF=8|m-1|•
=
,
设f(m)=3m3-5m2+m+1,(-
<m≤
),
则f'(m)=9m2-10m+1=0,解得m1=
,m2=1,
于是f(m)在(-
,
)是增函数,在(
,1)上是减函数,在(1,
)上是增函数,
又f(
)=
>f(
),
∴当m=
时,f(m)取得最大值
,此时k=±
,
∴△ABP面积的最大值为
.
设P(x0,y0),由抛物线的定义可知|PF|=y0+1,解得y0=2,
∴x0=±2
| 2 |
| 2 |
| 2 |
由
| PF |
| FM |
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
(Ⅱ)设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
由
|
于是△=16k2+16m>0,x1+x2=4k,x1x2=-4m,
即AB的中点M的坐标为(2k,2k2+m)
由
| PF |
| FM |
解得
|
| x | 2 0 |
| 1 |
| 5 |
| 4 |
| 15 |
由△>0,k>0得-
| 1 |
| 3 |
| 4 |
| 3 |
又∵|AB|=4
| 1+k2 |
| k2+m |
点F到直线AB的距离d=
| |m-1| | ||
|
∴S△ABP=4S△ABF=8|m-1|•
| k2+m |
| 16 | ||
|
| 3m3-5m2+m+1 |
设f(m)=3m3-5m2+m+1,(-
| 1 |
| 3 |
| 4 |
| 3 |
则f'(m)=9m2-10m+1=0,解得m1=
| 1 |
| 9 |
于是f(m)在(-
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
| 4 |
| 3 |
又f(
| 1 |
| 9 |
| 256 |
| 243 |
| 4 |
| 3 |
∴当m=
| 1 |
| 9 |
| 256 |
| 243 |
| ||
| 15 |
∴△ABP面积的最大值为
256
| ||
| 135 |
点评:本题主要考查抛物线的几何性质,直线和抛物线的位置关系,三角形面积公式,平面向量等基础知识,同时也考查解析几何的基本思想方法和运算求解能力.运算量大,综合性强,难度较大.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目