题目内容
已知函数f(x)定义在R上,对任意实数x有f(x+3)=-f(x)+2
,若函数y=f(x-1)的图象关于直线x=1对称,f(-1)=
,则f(2014)= .
| 2 |
| 2 |
考点:函数的值
专题:函数的性质及应用
分析:根据条件求出函数f(x)是偶函数,以及推断出函数的周期性,即可得到结论.
解答:
解:∵y=f(x-1)的图象关于直线x=1对称,
∴y=f(x)的图象关于直线x=0对称,即函数f(x)是偶函数,
∵f(x+3)=-f(x)+2
,
∴f(x+6)=-f(x+3)+2
=f(x),即函数的周期是6,
则f(2014)=f(336×6-2)=f(-2),
当x=-2时,f(-2+3)=-f(-2)+2
,
即f(1)=-f(-2)+2
,
∴f(-2)=2
-f(1)=2
-
=
,
故f(2014)=f(-2)=
,
故答案为:
.
∴y=f(x)的图象关于直线x=0对称,即函数f(x)是偶函数,
∵f(x+3)=-f(x)+2
| 2 |
∴f(x+6)=-f(x+3)+2
| 2 |
则f(2014)=f(336×6-2)=f(-2),
当x=-2时,f(-2+3)=-f(-2)+2
| 2 |
即f(1)=-f(-2)+2
| 2 |
∴f(-2)=2
| 2 |
| 2 |
| 2 |
| 2 |
故f(2014)=f(-2)=
| 2 |
故答案为:
| 2 |
点评:本题主要考查函数值的计算,根据条件判断函数的奇偶性和周期性是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知数列{an},an=-2n2+λn,若该数列是递减数列,则实数λ的取值范围是( )
| A、(-∞,6) |
| B、(-∞,4] |
| C、(-∞,5) |
| D、(-∞,3] |
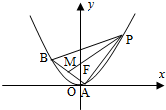 已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,
已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点, 某鲜花店对一个月的鲜花销售数量(单位:支)进行统计,统计时间是4月1日至4月30日,5天一组分组统计,绘制了如图的鲜花销售数量频率分布直方图.已知从左到右各长方形的高的比为2:3:4:6:4:1,且第二组的频数为180,那么该月共销售出的鲜花数(单位:支)为
某鲜花店对一个月的鲜花销售数量(单位:支)进行统计,统计时间是4月1日至4月30日,5天一组分组统计,绘制了如图的鲜花销售数量频率分布直方图.已知从左到右各长方形的高的比为2:3:4:6:4:1,且第二组的频数为180,那么该月共销售出的鲜花数(单位:支)为