题目内容
已知函数f(x)=x3+3|x-a|(a>0),若f(x)在[-1,1]上的最小值记为g(a).
(Ⅰ)求g(a);
(Ⅱ)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.
(Ⅰ)求g(a);
(Ⅱ)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)分类讨论,利用导数确定函数的单调性,即可求g(a);
(Ⅱ)设h(x)=f(x)-g(a),分类讨论,求最值,可以证明x∈[-1,1]时,恒有f(x)≤g(a)+4.
(Ⅱ)设h(x)=f(x)-g(a),分类讨论,求最值,可以证明x∈[-1,1]时,恒有f(x)≤g(a)+4.
解答:
(Ⅰ)解:∵a>0,-1≤x≤1,
①当0<a<1时,
若x∈[-1,a],则f(x)=x3-3x+3a,f′(x)=3x2-3<0,故此时函数在(-1,a)上是减函数,
若x∈(a,1],则f(x)=x3+3x-3a,f′(x)=3x2+3>0,故此时函数在(a,1)上是增函数,
∴g(a)=f(a)=a3.
②当a≥1,f(x)=x3+3|x-a|=x3-3x+3a,f′(x)=3x2-3<0,故此时函数在[-1,1]上是减函数,
则g(a)=f(1)=-2+3a.
综上:g(a)=
.
(Ⅱ)证明:设h(x)=f(x)-g(a),
①当0<a<1时,g(a)=a3,
若x∈[a,1],h(x)=x3+3x-3a-a3,h′(x)=3x2+3,
∴h(x)在[a,1]上是增函数,
∴h(x)在[a,1]上的最大值是h(1)=4-3a-a3,且0<a<1,∴h(1)≤4,∴f(x)≤g(a)+4.
若x∈[-1,a],h(x)=x3-3x+3a-a3,h′(x)=3x2-3,
∴h(x)在[-1,a]上是减函数,
∴h(x)在[-1,a]上的最大值是h(-1)=2+3a-a3,
令t(a)=2+3a-a3,则t′(a)=3-3a2,∴t(a)在(0,1)上是增函数,
∴t(a)<t(1)=4
∴h(-1)<4,∴f(x)≤g(a)+4.
③a≥1时,g(a)=-2+3a,∴h(x)=x3-3x+2,∴h′(x)=3x2-3,
∴h(x)在[-1,1]上是减函数,
∴h(x)在[-1,1]上的最大值是h(-1)=4,
∴f(x)≤g(a)+4;
综上,当x∈[-1,1]时,恒有f(x)≤g(a)+4.
①当0<a<1时,
若x∈[-1,a],则f(x)=x3-3x+3a,f′(x)=3x2-3<0,故此时函数在(-1,a)上是减函数,
若x∈(a,1],则f(x)=x3+3x-3a,f′(x)=3x2+3>0,故此时函数在(a,1)上是增函数,
∴g(a)=f(a)=a3.
②当a≥1,f(x)=x3+3|x-a|=x3-3x+3a,f′(x)=3x2-3<0,故此时函数在[-1,1]上是减函数,
则g(a)=f(1)=-2+3a.
综上:g(a)=
|
(Ⅱ)证明:设h(x)=f(x)-g(a),
①当0<a<1时,g(a)=a3,
若x∈[a,1],h(x)=x3+3x-3a-a3,h′(x)=3x2+3,
∴h(x)在[a,1]上是增函数,
∴h(x)在[a,1]上的最大值是h(1)=4-3a-a3,且0<a<1,∴h(1)≤4,∴f(x)≤g(a)+4.
若x∈[-1,a],h(x)=x3-3x+3a-a3,h′(x)=3x2-3,
∴h(x)在[-1,a]上是减函数,
∴h(x)在[-1,a]上的最大值是h(-1)=2+3a-a3,
令t(a)=2+3a-a3,则t′(a)=3-3a2,∴t(a)在(0,1)上是增函数,
∴t(a)<t(1)=4
∴h(-1)<4,∴f(x)≤g(a)+4.
③a≥1时,g(a)=-2+3a,∴h(x)=x3-3x+2,∴h′(x)=3x2-3,
∴h(x)在[-1,1]上是减函数,
∴h(x)在[-1,1]上的最大值是h(-1)=4,
∴f(x)≤g(a)+4;
综上,当x∈[-1,1]时,恒有f(x)≤g(a)+4.
点评:利用导数可以解决最值问题,正确求导,确定函数的单调性是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
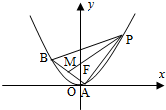 已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,
已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点, 某鲜花店对一个月的鲜花销售数量(单位:支)进行统计,统计时间是4月1日至4月30日,5天一组分组统计,绘制了如图的鲜花销售数量频率分布直方图.已知从左到右各长方形的高的比为2:3:4:6:4:1,且第二组的频数为180,那么该月共销售出的鲜花数(单位:支)为
某鲜花店对一个月的鲜花销售数量(单位:支)进行统计,统计时间是4月1日至4月30日,5天一组分组统计,绘制了如图的鲜花销售数量频率分布直方图.已知从左到右各长方形的高的比为2:3:4:6:4:1,且第二组的频数为180,那么该月共销售出的鲜花数(单位:支)为