题目内容
设函数f(x)=丨x+1丨+丨x-2丨-m.
(Ⅰ)当m=5时,求f(x)>0的解集;
(Ⅱ)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
(Ⅰ)当m=5时,求f(x)>0的解集;
(Ⅱ)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)当m=5时,把不等式转化为与之等价的三个不等式组,求得美俄不等式组的解集,再取并集,即得所求.
(Ⅱ)由题意可得丨x+1丨+丨x-2丨-m的最小值大于或等于2,由绝对值三角不等式可得丨x+1丨+丨x-2丨-m的最小值为3,可得3-m≥2,从而求得m的范围.
(Ⅱ)由题意可得丨x+1丨+丨x-2丨-m的最小值大于或等于2,由绝对值三角不等式可得丨x+1丨+丨x-2丨-m的最小值为3,可得3-m≥2,从而求得m的范围.
解答:
解:(Ⅰ)当m=5时,函数f(x)=丨x+1丨+丨x-2丨-5,
由f(x)>0可得
①,或
,或 ②
.
解①求得 x>3,解②求得x∈∅,解③求得x<-2.
(Ⅱ)若关于x的不等式f(x)≥2的解集是R,即 丨x+1丨+丨x-2丨≥2+m 的解集为R.
而丨x+1丨+丨x-2丨≥|(x+1)-(x-2)|=3,
故有 3≥2+m,即 m≤1,
故m的范围为(-∞,1].
由f(x)>0可得
|
|
|
解①求得 x>3,解②求得x∈∅,解③求得x<-2.
(Ⅱ)若关于x的不等式f(x)≥2的解集是R,即 丨x+1丨+丨x-2丨≥2+m 的解集为R.
而丨x+1丨+丨x-2丨≥|(x+1)-(x-2)|=3,
故有 3≥2+m,即 m≤1,
故m的范围为(-∞,1].
点评:本题主要考查绝对值不等式的解法,绝对值三角不等式,体现了等价转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
若复数z=(a2-2)+(a+
)i为纯虚数(a∈R),则复数
位于( )
| 2 |
| a-i |
| a+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
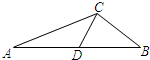 如图,在△ABC中,|
如图,在△ABC中,|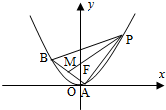 已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,
已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,