题目内容
已知矩阵A=
,求点M(-1,1)在矩阵A-1对应的变换作用下得到的点M′坐标.
|
考点:逆变换与逆矩阵
专题:矩阵和变换
分析:利用公式求出A的逆矩阵A-1,进而即可求出点M(-1,1)在矩阵A-1对应的变换作用下得到的点M′坐标.
解答:
解:设A-1=
,则AA-1=
=
,
所以
c=1,
d=0,a-
c=0,b-
d=1,
解得a=2,b=1,c=3,d=0,
即A-1=
.
由
=
,知点M′(-1,-3),
所以新坐标为M′(-1,-3).
|
|
|
|
所以
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解得a=2,b=1,c=3,d=0,
即A-1=
|
由
|
|
|
所以新坐标为M′(-1,-3).
点评:本题以点的变换为载体,考查待定系数法求矩阵,解题的关键是构建方程组.

练习册系列答案
相关题目
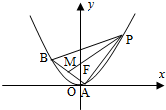 已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,
已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,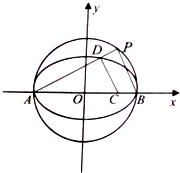 已知椭圆E:
已知椭圆E: