题目内容
已知集合A={（x，y）|x2+y2≤2，x∈Z，y∈Z}，则从A中任选一个元素（x，y）满足x+y≥1的概率为 ．
考点：古典概型及其概率计算公式,几何概型
专题：概率与统计
分析：利用枚举法确定满足A以及x+y≥1的点的个数，根据古典概型概率公式，可得结论．
解答：
解：满足A={（x，y）|x2+y2≤2，x∈Z，y∈Z}的点有：
（-1，-1），（-1，0），（-1，1），
（0，-1），（0，0），（0，1），
（1，-1），（1，0），（1，1），共9个，
则从A中任选一个元素（x，y）满足x+y≥1的有：
（0，1），（1，0），（1，1），共3个，
则从A中任选一个元素（x，y）满足x+y≥1的概率为
．
故答案为：
．
（-1，-1），（-1，0），（-1，1），
（0，-1），（0，0），（0，1），
（1，-1），（1，0），（1，1），共9个，
则从A中任选一个元素（x，y）满足x+y≥1的有：
（0，1），（1，0），（1，1），共3个，
则从A中任选一个元素（x，y）满足x+y≥1的概率为
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查古典概型求概率的办法，确定基本事件的个数是关键．
练习册系列答案
名校课堂系列答案
相关题目
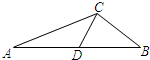如图，在△ABC中，|
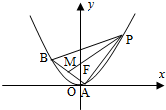已知△ABP的三个顶点在抛物线C：x2=4y上，F为抛物线C的焦点，点M为AB的中点，