题目内容
设函数f(x)=x2+ax-2lnx,常数a∈R
(1)求f(x)的单调区间;
(2)设-3<a<3,记f(x)的极小值为fmin(x),若不等式b-2ln2<f(x)min<b+4-2ln2恒成立,求b的取值范围.
(1)求f(x)的单调区间;
(2)设-3<a<3,记f(x)的极小值为fmin(x),若不等式b-2ln2<f(x)min<b+4-2ln2恒成立,求b的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)写出函数f(x)的定义域,求出f'(x),通过解不等式f'(x)>0,f'(x)<0可得单调区间;
(2)不等式b-2ln2<f(x)min<b+4-2ln2恒成立,只要求出f(x)的最小值,从而求出实数b的取值范围;
(2)不等式b-2ln2<f(x)min<b+4-2ln2恒成立,只要求出f(x)的最小值,从而求出实数b的取值范围;
解答:
解:(1)f′(x)=
(x>0,a∈R),
注意到-a-
<0<-a+
则f(x)在(0,
)单调递减,(
,+∞)单调递增
(2)设极小值点为x=t,则f′(t)=0
∴2t2+at-2=0
∴a=
,
根据|a|<3
∴
<3
∴(2t2-2)2-(3t)2<0(t>0)
∴t∈(
,2)
此时f极小(x)=f(t)=t2+at-2lnt=t2+t?
-2lnt=2-t2-2lnt,t∈(
,2)
设g(t)=2-t2-2lnt,t∈(
,2)
∴g′(t)=-
<0
∴g(t)在(
,2)单调递减
∴g(2)<g(t)<g(
)
∴g(t)∈(-2-2ln2,
+2ln2)
∴-2-2ln2<f极小(x)<
+2ln2
故“b-2ln2≤-2-2ln2”且“
+2ln2≤b+4+2ln2”
∴b∈[-
,-2]
| 2x2+ax-2 |
| x |
注意到-a-
| a2+16 |
| a2+16 |
则f(x)在(0,
-a+
| ||
| 4 |
-a+
| ||
| 4 |
(2)设极小值点为x=t,则f′(t)=0
∴2t2+at-2=0
∴a=
| 2-2t2 |
| t |
根据|a|<3
∴
| |2-2t2| |
| |t| |
∴(2t2-2)2-(3t)2<0(t>0)
∴t∈(
| 1 |
| 2 |
此时f极小(x)=f(t)=t2+at-2lnt=t2+t?
| 2-2t2 |
| t |
| 1 |
| 2 |
设g(t)=2-t2-2lnt,t∈(
| 1 |
| 2 |
∴g′(t)=-
| 2(t2+1) |
| t |
∴g(t)在(
| 1 |
| 2 |
∴g(2)<g(t)<g(
| 1 |
| 2 |
∴g(t)∈(-2-2ln2,
| 7 |
| 4 |
∴-2-2ln2<f极小(x)<
| 7 |
| 4 |
故“b-2ln2≤-2-2ln2”且“
| 7 |
| 4 |
∴b∈[-
| 9 |
| 4 |
点评:本题考查利用导数研究函数的单调性、零点及不等式的证明等知识,考查学生综合运用知识分析解决问题的能力、推理论证能力,本题综合性强,能力要求较高.

练习册系列答案
相关题目
不等式|3-2x|<1的解集为( )
| A、(-2,2) |
| B、(2,3) |
| C、(1,2) |
| D、(3,4) |
集合A={a2,a+1,-3},B={a-3,a2+1,2a-1},且A∩B={-3}.则a=( )
| A、-1 | B、0 |
| C、0 或-1 | D、2 |
若复数z=(a2-2)+(a+
)i为纯虚数(a∈R),则复数
位于( )
| 2 |
| a-i |
| a+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
为得到函数y=cosx的图象,只需将函数y=sinx的图象按照向量
平移,则
可以为( )
| a |
| a |
A、(
| ||
B、(-
| ||
C、(0,-
| ||
D、(0,
|
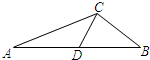 如图,在△ABC中,|
如图,在△ABC中,|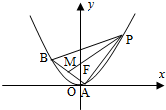 已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,
已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,