题目内容
对于函数f(x)=a-
(a∈R).
(1)探索并证明函数f(x)的单调性;
(2)是否存在实数a使函数f(x)为奇函数?若有,求出实数a的值,并证明你的结论;若没有,说明理由.
| 2 |
| 2x+1 |
(1)探索并证明函数f(x)的单调性;
(2)是否存在实数a使函数f(x)为奇函数?若有,求出实数a的值,并证明你的结论;若没有,说明理由.
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用导数判断函数的单调性即可;
(2)先由f(0)=0求得a=1,再证明f(-x)=-f(x),恒成立.
(2)先由f(0)=0求得a=1,再证明f(-x)=-f(x),恒成立.
解答:
解:∵f(x)=a-
(a∈R).
∴f′(x)=
>0恒成立,
∴函数f(x)在R上为增函数
(2)由f(0)=a-
=0,得a=1,
∴f(x)=1-
=
,
∵f(-x)=
=
=-
=-f(x)
所以当a=1时,f(x)为奇函数.
| 2 |
| 2x+1 |
∴f′(x)=
| 2ln2•2x |
| (2x+1)2 |
∴函数f(x)在R上为增函数
(2)由f(0)=a-
| 2 |
| 20+1 |
∴f(x)=1-
| 2 |
| 2x+1 |
| 2x-1 |
| 2x+1 |
∵f(-x)=
| 2-x-1 |
| 2-x+1 |
| 1-2x |
| 1+2x |
| 2x-1 |
| 2x+1 |
所以当a=1时,f(x)为奇函数.
点评:本题主要考查了导数与函数的单调性的关系以及函数的奇偶性,属于基础题.

练习册系列答案
相关题目
一个不透明的盒子里有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.那么甲赢的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、以上均不对 |
以圆 (x-1)2+y2=2的圆心为抛物线的焦点,且顶点为坐标原点的抛物线方程为( )
| A、y2=4x |
| B、y2=2x |
| C、x2=4y |
| D、x2=2y |
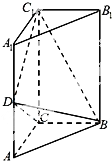 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=2,BC=4,AA1=4,D是棱AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=2,BC=4,AA1=4,D是棱AA1的中点.