题目内容
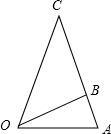 在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+
在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+| 3 |
(1)将y表示成x的函数;
(2)当x取何值时,△AOC的面积最小?最小值是多少平方米?
考点:解三角形的实际应用
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由图形知,S△BOC+S△AOB=S△AOC,代入面积公式,求出函数y的解析式;
(2)由(1)知,函数y的解析式,求出S△AOC的表达式,利用基本不等式求出S△OAC最小时,x的取值以及最小面积是什么.
(2)由(1)知,函数y的解析式,求出S△AOC的表达式,利用基本不等式求出S△OAC最小时,x的取值以及最小面积是什么.
解答:
解:(1)结合图形可知,S△BOC+S△AOB=S△AOC.
∴
(1+
)sin30°+
y(1+
)sin45°=
xysin75°,
解得:y=
,(其中3≤x≤6).
(2)由(1)知,y=
,(3≤x≤6),
因此,S△AOC=
xysin75°=
•
=
[(x-2)+
+4]≥2+2
,(当且仅当x-2=
,即x=4时,等号成立).
∴当x=400米时,整个中转站的占地面积S△OAC最小,最小面积是(2+2
)×104平方米.
∴
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
解得:y=
| ||
| x-2 |
(2)由(1)知,y=
| ||
| x-2 |
因此,S△AOC=
| 1 |
| 2 |
1+
| ||
| 4 |
| x2 |
| x-2 |
1+
| ||
| 4 |
| 4 |
| x-2 |
| 3 |
| 4 |
| x-2 |
∴当x=400米时,整个中转站的占地面积S△OAC最小,最小面积是(2+2
| 3 |
点评:本题考查了求函数的解析式以及利用基本不等式求函数的最值问题,解题时应根据题意,列出等量关系,求出函数的解析式,是综合题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
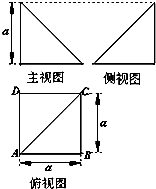 四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )A、(2
| ||
| B、2a2 | ||
C、(1+
| ||
D、(2+
|
 一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:(其中i=1,2,3,4,5,6,7,).
一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:(其中i=1,2,3,4,5,6,7,).

 如图,四棱锥V-ABCD的底面为矩形,侧面VAB⊥底面ABCD,又VB⊥平面VAD,求证:平面VBC⊥平面VAC.
如图,四棱锥V-ABCD的底面为矩形,侧面VAB⊥底面ABCD,又VB⊥平面VAD,求证:平面VBC⊥平面VAC.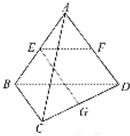 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F分别是AB、AD的中点,则
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F分别是AB、AD的中点,则