题目内容
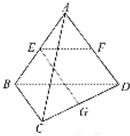 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F分别是AB、AD的中点,则
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F分别是AB、AD的中点,则| BF |
| CE |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用向量的中点表示形式,以及向量的数量积的定义,即可计算得到.
解答:
解:由于F为AD的中点,
则
=
+
=
+
=
(
+
),
由于E为AB的中点,
则
=
(
+
)=
(-2
+
),
则有
•
=
(-2
•
+
2+
•
-2
•
)
=
(-2×1×1×cos60°+1+1×1×cos60°-2×1×1×cos60°)
=
×(-1+1+
-1)=-
.
故答案为:-
.
则
| BF |
| BA |
| AF |
| BA |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| BA |
| BD |
由于E为AB的中点,
则
| CE |
| 1 |
| 2 |
| CB |
| CA |
| 1 |
| 2 |
| BC |
| BA |
则有
| BF |
| CE |
| 1 |
| 4 |
| BC |
| BA |
| BA |
| BA |
| BD |
| BC |
| BD |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
故答案为:-
| 1 |
| 8 |
点评:本题考查平面向量的数量积的定义和性质,考查中点的斜率表示形式,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知a,b是异面直线,直线c∥a,那么c与b( )
| A、一定是异面 |
| B、一定是相交直线 |
| C、不可能是相交直线 |
| D、不可能是平行直线 |
已知函数f(x)=-x2+ax+b2-b+1(a∈R,b∈R),对任意实数x都有f(1-x)=f(1+x)成立,若当x∈[-1,1]时,f(x)>0恒成立,则b的取值范围是( )
| A、b<-1或 b>2 |
| B、b>2 |
| C、-1<b<0 |
| D、不能确定 |
若曲线y=
x3+
x2+1在x=1处的切线与直线2x+my+1=0平行,则实数m的值等于( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、-2 | B、-1 | C、1 | D、2 |
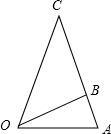 在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+
在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+ 如图,已知正方形ABCD的边长为l,点E是AB边上的动点.则
如图,已知正方形ABCD的边长为l,点E是AB边上的动点.则