题目内容
 一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:(其中i=1,2,3,4,5,6,7,).
一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:(其中i=1,2,3,4,5,6,7,).| 人数xi | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 件数yi | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
(Ⅱ)求回归直线方程.(结果保留到小数点后两位)
(参考数据:
| 7 |
 |
| i=1 |
. |
| x |
. |
| y |
| 7 |
 |
| i=1 |
2 i |
. |
| x |
. |
| x |
. |
| y |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
(Ⅲ)预测进店人数为80人时,商品销售的件数.(结果保留整数)
考点:线性回归方程
专题:综合题,概率与统计
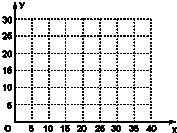
分析:(I)根据所给的这一组数据,得到7个点的坐标,把这几个点的坐标在直角坐标系中描出对应的点,得到散点图,从散点图可以看出,这两个两之间是正相关.
(II)根据所给的数据,做出x,y的平均数,即得到这组数据的样本中心点,根据最小二乘法做出线性回归方程的系数,写出线性回归方程.
(III)利用上一问做出的线性回归方程,把x的值代入方程,预报出对应的y的值.
(II)根据所给的数据,做出x,y的平均数,即得到这组数据的样本中心点,根据最小二乘法做出线性回归方程的系数,写出线性回归方程.
(III)利用上一问做出的线性回归方程,把x的值代入方程,预报出对应的y的值.
解答:
 解:(Ⅰ)散点图如图…(4分)
解:(Ⅰ)散点图如图…(4分)
(Ⅱ)∵
xiyi=3245,
=25,
=15.43,
x
=5075,7(
)2=4375,
=2695,
∴
=≈0.79,…(6分)
a=-4.32…(8分)
∴回归直线方程是y=0.79x-4.32…(9分)
(Ⅲ).进店人数80人时,商品销售的件数y=0.79×80-4.32≈59件…(12分)
 解:(Ⅰ)散点图如图…(4分)
解:(Ⅰ)散点图如图…(4分)(Ⅱ)∵
| 7 |
 |
| i=1 |
. |
| x |
. |
| y |
| 7 |
 |
| i=1 |
2 i |
. |
| x |
. |
| x |
. |
| y |
∴
 |
| b |
a=-4.32…(8分)
∴回归直线方程是y=0.79x-4.32…(9分)
(Ⅲ).进店人数80人时,商品销售的件数y=0.79×80-4.32≈59件…(12分)
点评:本题考查线性回归方程,考查最小二乘法求线性回归方程的系数,考查样本中心点的求法,本题的运算量比较大,是一个综合题目,

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知数列{an}前n项和为Sn,且a1=1,Sn=n2an,n∈N*试归纳猜想出Sn的表达式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b是异面直线,直线c∥a,那么c与b( )
| A、一定是异面 |
| B、一定是相交直线 |
| C、不可能是相交直线 |
| D、不可能是平行直线 |
已知函数f(x)=-x2+ax+b2-b+1(a∈R,b∈R),对任意实数x都有f(1-x)=f(1+x)成立,若当x∈[-1,1]时,f(x)>0恒成立,则b的取值范围是( )
| A、b<-1或 b>2 |
| B、b>2 |
| C、-1<b<0 |
| D、不能确定 |
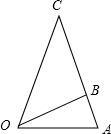 在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+
在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+