题目内容
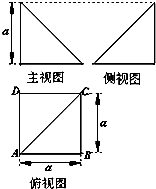 四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )A、(2
| ||
| B、2a2 | ||
C、(1+
| ||
D、(2+
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,我们易得PA是棱锥的高,由三视图我们易得底面边长,及棱锥的高均为a,由此我们易求出各棱的长,进而求出各个面的面积,进而求出四棱锥P-ABCD的表面积.
解答:
解:由三视图我们易得四棱锥P-ABCD的底面棱长为a,高PA=a
则四棱锥P-ABCD的底面积为:a2
侧面积为:S△PAB+S△PBC+S△PCD+S△PAD=2×
×a2=2×
×a×
a=(2+
)a2,
则四棱锥P-ABCD的表面积为(2+
)a2.
故选D.
则四棱锥P-ABCD的底面积为:a2
侧面积为:S△PAB+S△PBC+S△PCD+S△PAD=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
则四棱锥P-ABCD的表面积为(2+
| 2 |
故选D.
点评:本题考查由三视图求几何体的表面积,考查由三视图看出几何体中各个部分的长度,本题是一个基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
抛物线y=-2x2的焦点坐标是( )
A、(-
| ||
| B、(-1,0) | ||
C、(0,-
| ||
D、(0,-
|
已知数列{an}前n项和为Sn,且a1=1,Sn=n2an,n∈N*试归纳猜想出Sn的表达式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
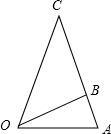 在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+
在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+