题目内容
已知函数f(x)=|x-m|-2|x-1|.
(1)当m=3时,求f(x)的最大值;
(2)解关于x的不等式f(x)≥0.
(1)当m=3时,求f(x)的最大值;
(2)解关于x的不等式f(x)≥0.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)当m=3时,函数f(x)=|x-3|-2|x-1|=
,再根据函数的单调性求得函数f(x)的最大值.
(2)关于x的不等式即 (x-m)2≥4(x-1)2,化简可得3x2+(2m-8)x+4-m2≤0.计算△=16(m-1)2≥0,由此求得一元二次不等式的解集.
|
(2)关于x的不等式即 (x-m)2≥4(x-1)2,化简可得3x2+(2m-8)x+4-m2≤0.计算△=16(m-1)2≥0,由此求得一元二次不等式的解集.
解答:
解:(1)当m=3时,函数f(x)=|x-3|-2|x-1|=
,故当x=1时,函数f(x)取得最大值为2.
(2)关于x的不等式f(x)≥0,即|x-m|≥2|x-1|,即 (x-m)2≥4(x-1)2,化简可得3x2+(2m-8)x+4-m2≤0.
由于△=16(m-1)2≥0,求得
≤x≤
.
|
(2)关于x的不等式f(x)≥0,即|x-m|≥2|x-1|,即 (x-m)2≥4(x-1)2,化简可得3x2+(2m-8)x+4-m2≤0.
由于△=16(m-1)2≥0,求得
| 4-m-2|m-1| |
| 2 |
| 4-m+2|m-1| |
| 2 |
点评:本题主要考查带有绝对值的函数,绝对值不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知
、
是两个不平行的非零向量,并且
∥
,
∥
,则向量
等于( )
| a |
| b |
| a |
| c |
| b |
| c |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
抛物线y=-2x2的焦点坐标是( )
A、(-
| ||
| B、(-1,0) | ||
C、(0,-
| ||
D、(0,-
|
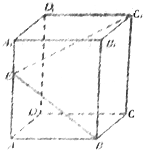 长方体ABCD-A1B1C1D1的底面是边长为a的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值为( )
长方体ABCD-A1B1C1D1的底面是边长为a的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值为( )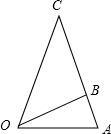 在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+
在△OAC地段中,OB是连接△OBC与△OAB的一条道路,且OB=(1+