题目内容
求经过点M（3，-1）且与圆C：x2+y2+2x-6y+5=0相切于点N（1，2）的圆的方程．
考点：圆的切线方程
专题：计算题,直线与圆
分析：先利用待定系数法假设圆的标准方程：（x-a）2+（y-b）2=r2，求出已知圆的圆心坐标与半径，再根据条件圆C过点M（3，-1）且与圆x2+y2+2x-6y+5=0相切于点N（1，2），列出方程组可求相应参数，从而可求方程．
解答：
解：设所求圆方程：（x-a）2+（y-b）2=r2
已知圆的圆心：（-1，3），半径=
，
由题意可得：（3-a）2+（-1-b）2=r2，（1-a）2+（2-b）2=r2，（a+1）2+（b-3）2=(
+r)2，
解得a=
，b=
，r2=
∴所求圆：（x-
）2+（y-
）2=
．
已知圆的圆心：（-1，3），半径=
| 5 |
由题意可得：（3-a）2+（-1-b）2=r2，（1-a）2+（2-b）2=r2，（a+1）2+（b-3）2=(
| 5 |
解得a=
| 20 |
| 7 |
| 15 |
| 14 |
| 845 |
| 196 |
∴所求圆：（x-
| 20 |
| 7 |
| 15 |
| 14 |
| 845 |
| 196 |
点评：本题的考点是圆的标准方程，主要考查利用待定系数法求圆的标准方程，考查学生分析解决问题的能力．
练习册系列答案
活力课时同步练习册系列答案
相关题目
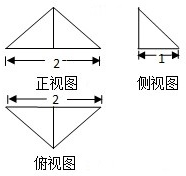一个几何体的三视图及部分数据如图所示，正视图、侧视图和俯视图都是等腰直角三角形，则该几何体的外接球体积为