题目内容
已知{an}为等比数列,其中a1=1,且a2,a3+a5,a4成等差数列.
(1)求数列{an}的通项公式:
(2)设bn=(2n-1)•an,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式:
(2)设bn=(2n-1)•an,求数列{bn}的前n项和Tn.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知条件,利用等比数列的通项公式和等差数列的性质求出等比数列的公比,由此能求出数列{
}的通项公式.
(2)由数列{
}的通项公式和bn=(2n-1)•an,求出bn=(2n-1)•(
)n-1,由此利用错位相减求和法能求出
数列{bn}的前n项和Tn.
| a | n |
(2)由数列{
| a | n |
| 1 |
| 2 |
数列{bn}的前n项和Tn.
解答:
解:(1)设在等比数列{an}中,公比为q,
∵a1=1,且a2,a3+a5,a4成等差数列,
∴2(a3+a5)=a2+a4,
∴2(q2+q4)=q+q3,
解得q=
,
∴an=(
)n-1.
(2)∵an=(
)n-1,
∴bn=(2n-1)•an=(2n-1)•(
)n-1,
∴Tn =1•1+3•
+5•(
)2+…+(2n-1)•(
)n-1,①
Tn=1•
+3•(
)2+5•(
)3+…+(2n-1)•(
)n,②
①-②,得:
Tn=1+2•[
+(
)2+…+(
)n-1]-(2n-1)•(
)n
=1+2[1-(
)n-1]-(2n-1)•(
)n
=3-
,
∴Tn=6-
.
∵a1=1,且a2,a3+a5,a4成等差数列,
∴2(a3+a5)=a2+a4,
∴2(q2+q4)=q+q3,
解得q=
| 1 |
| 2 |
∴an=(
| 1 |
| 2 |
(2)∵an=(
| 1 |
| 2 |
∴bn=(2n-1)•an=(2n-1)•(
| 1 |
| 2 |
∴Tn =1•1+3•
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②,得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+2[1-(
| 1 |
| 2 |
| 1 |
| 2 |
=3-
| 2n+3 |
| 2n |
∴Tn=6-
| 2n+3 |
| 2n-1 |
点评:本题考查数列的通项公式和前n项和的求法,是中档题,解题时要熟练掌握等比数列、等差数列的性质,注意错位相减法的合理运用.

练习册系列答案
相关题目
已知正方体的棱长为2,则外接球的表面积和体积( )
A、48π,32
| ||
B、48π,4
| ||
C、12π,4
| ||
D、12π,32
|
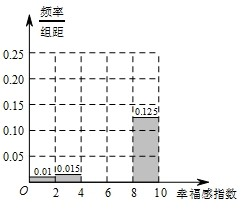 前不久央视记者就“你幸福吗?”采访了走在接头及工作岗位上的部分人员.人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.为了解某地区居民的幸福感,随机对该地区的男、女居民各500人进行了调查,调查数据如表所示:
前不久央视记者就“你幸福吗?”采访了走在接头及工作岗位上的部分人员.人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.为了解某地区居民的幸福感,随机对该地区的男、女居民各500人进行了调查,调查数据如表所示: