题目内容
设函数f（x）是定义域为x∈R且x≠0上的奇函数，当x＞0时，f(x)=
．
（1）写出x＜0时，函数f（x）的解析式；
（2）解不等式：f(x)＜-
．
| x |
| 1-2x |
（1）写出x＜0时，函数f（x）的解析式；
（2）解不等式：f(x)＜-
| x |
| 3 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：（1）根据函数奇偶性的对称性即可求出函数f（x）的解析式；
（2）根据函数的不等式解不等式即可．
（2）根据函数的不等式解不等式即可．
解答：
解：（1）：∵f（x）是R上的奇函数，
∴f（0）=0，
设x＜0，则-x＞0，
∵当x＞0时，f(x)=
．
∴f（-x）=
=
=-f（x），
∴f(x)=x•
，（x＜0）．
（2）当x＞0时，f(x)=
＜-
，解得0＜x＜2，
当x＜0时，f(x)=x•
＜-
，解得x＜-2，
综上得x∈（-∞，-2）∪（0，2）．
∴f（0）=0，
设x＜0，则-x＞0，
∵当x＞0时，f(x)=
| x |
| 1-2x |
∴f（-x）=
| -x |
| 1-2-x |
| -x•2x |
| 2x-1 |
∴f(x)=x•
| 2x |
| 2x-1 |
（2）当x＞0时，f(x)=
| x |
| 1-2x |
| x |
| 3 |
当x＜0时，f(x)=x•
| 2x |
| 2x-1 |
| x |
| 3 |
综上得x∈（-∞，-2）∪（0，2）．
点评：本题主要考查函数奇偶性的应用以及不等式的解法，利用函数的奇偶性求出函数的表达式是解决本题的关键．
练习册系列答案
相关题目
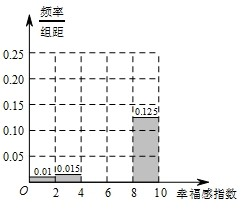前不久央视记者就“你幸福吗？”采访了走在接头及工作岗位上的部分人员．人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度，常用区间[0，10]内的一个数来表示，该数越接近10表示满意度越高．为了解某地区居民的幸福感，随机对该地区的男、女居民各500人进行了调查，调查数据如表所示：