题目内容
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为y=
x,它的一个焦点在抛物线y2=12x的准线上,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线的焦点,可得双曲线中的c,利用双曲线的一条渐近线方程为y=
x,可得
=
,即可求出a,b,从而可得双曲线的方程.
| 2 |
| b |
| a |
| 2 |
解答:
解:抛物线y2=12x的准线方程为x=-3,
∵双曲线的一个焦点在抛物线y2=12x的准线上,
∴c=3,
∵双曲线的一条渐近线方程为y=
x,
∴
=
,
∴a=
,b=
,
∴双曲线的方程为
2-
2=1.
故选:A.
∵双曲线的一个焦点在抛物线y2=12x的准线上,
∴c=3,
∵双曲线的一条渐近线方程为y=
| 2 |
∴
| b |
| a |
| 2 |
∴a=
| 3 |
| 6 |
∴双曲线的方程为
| x |
| 3 |
| y |
| 6 |
故选:A.
点评:本题考查抛物线、双曲线的性质,考查双曲线的方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知全集U=R,N={x|x(x+3)<0},M={x|x<-1}则图中阴影部分表示的集合是( )


| A、{x|-3<x<-1} |
| B、{x|-3<x<0} |
| C、{x|-1≤x<0} |
| D、{x<-3} |
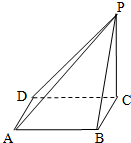 如图,四棱锥P-ABCD的底面是正方形,PC⊥底面ABCD.
如图,四棱锥P-ABCD的底面是正方形,PC⊥底面ABCD.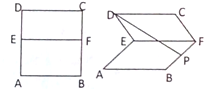 已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是
已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是