题目内容
已知a∈{x|(
)x-x=0},则f(x)=loga(x2-2x-3)的减区间为 .
| 1 |
| 3 |
考点:函数的值域
专题:函数的性质及应用
分析:本题可以先将已知集合时行化简,得到参数a的取值范围,再求出函数f(x)的定义域,根据复合函数单调性的判断规律,求出f(x)的单调区间,得到本题结论.
解答:
解:∵(
)x-x=0
∴(
)x=x,
当x>1时,(
)x<(
)1<1,方程(
)x=x不成立,
当x=1时,方程(
)x=x显然不成立,
当x<0时,方程(
)x>0,方程(
)x=x不成立,
当x=0时,方程(
)x=x显然不成立,
∴0<x<1.
∵函数f(x)=loga(x2-2x-3)中,x2-2x-3>0,
∴x<-1或x>3.
当x∈(-∞,-1)时,y=x2-2x-3单调递减,f(x)=loga(x2-2x-3)单调递增;
当x∈(3,+∞)时,y=x2-2x-3单调递增,f(x)=loga(x2-2x-3)单调递减.
∴f(x)=loga(x2-2x-3)的减区间为(3,+∞).
故答案为:(3,+∞).
| 1 |
| 3 |
∴(
| 1 |
| 3 |
当x>1时,(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
当x=1时,方程(
| 1 |
| 3 |
当x<0时,方程(
| 1 |
| 3 |
| 1 |
| 3 |
当x=0时,方程(
| 1 |
| 3 |
∴0<x<1.
∵函数f(x)=loga(x2-2x-3)中,x2-2x-3>0,
∴x<-1或x>3.
当x∈(-∞,-1)时,y=x2-2x-3单调递减,f(x)=loga(x2-2x-3)单调递增;
当x∈(3,+∞)时,y=x2-2x-3单调递增,f(x)=loga(x2-2x-3)单调递减.
∴f(x)=loga(x2-2x-3)的减区间为(3,+∞).
故答案为:(3,+∞).
点评:本题考查了指数方程、函数的定义域、函数的单调性,本题难度不大,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为y=
x,它的一个焦点在抛物线y2=12x的准线上,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
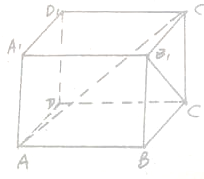 已知长方体AC1中,AB=BC=4cm,AA1=2cm,E,F分别为BB1和A1B1的中点,求:
已知长方体AC1中,AB=BC=4cm,AA1=2cm,E,F分别为BB1和A1B1的中点,求: