题目内容
已知asinA+cosA=1,bsinA-cosA=1,求ab的值.
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由条件求得a=
,b=
,再利用同角三角函数的基本关系求得ab的值.
| 1-cosA |
| sinA |
| 1+cosA |
| sinA |
解答:
解:∵已知asinA+cosA=1,bsinA-cosA=1,∴a=
,b=
,∴ab=
=1.
| 1-cosA |
| sinA |
| 1+cosA |
| sinA |
| 1-cos2A |
| sin2A |
点评:本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知点p(-1,-
)在角θ的终边上,且θ∈[0,2π),则θ的值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为y=
x,它的一个焦点在抛物线y2=12x的准线上,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
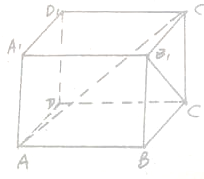 已知长方体AC1中,AB=BC=4cm,AA1=2cm,E,F分别为BB1和A1B1的中点,求:
已知长方体AC1中,AB=BC=4cm,AA1=2cm,E,F分别为BB1和A1B1的中点,求: